| < Day Day Up > |
Although hashing is most often used for its excellent expected performance, hashing can be used to obtain excellent worst-case performance when the set of keys is static: once the keys are stored in the table, the set of keys never changes. Some applications naturally have static sets of keys: consider the set of reserved words in a programming language, or the set of file names on a CD-ROM. We call a hashing technique perfect hashing if the worst-case number of memory accesses required to perform a search is O(1).
The basic idea to create a perfect hashing scheme is simple. We use a two-level hashing scheme with universal hashing at each level. Figure 11.6 illustrates the approach.
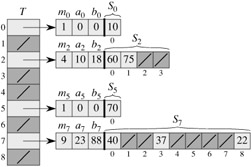
The first level is essentially the same as for hashing with chaining: the n keys are hashed into m slots using a hash function h carefully selected from a family of universal hash functions.
Instead of making a list of the keys hashing to slot j, however, we use a small secondary hash table Sj with an associated hash function hj. By choosing the hash functions hj carefully, we can guarantee that there are no collisions at the secondary level.
In order to guarantee that there are no collisions at the secondary level, however, we will need to let the size mj of hash table Sj be the square of the number nj of keys hashing to slot j. While having such a quadratic dependence of mj on nj may seem likely to cause the overall storage requirements to be excessive, we shall show that by choosing the first level hash function well, the expected total amount of space used is still O(n).
We use hash functions chosen from the universal classes of hash functions of Section 11.3.3. The first-level hash function is chosen from the class ℋp,m, where as in Section 11.3.3, p is a prime number greater than any key value. Those keys hashing to slot j are re-hashed into a secondary hash table Sj of size mj using a hash function hj chosen from the class ![]() .[1]
.[1]
We shall proceed in two steps. First, we shall determine how to ensure that the secondary tables have no collisions. Second, we shall show that the expected amount of memory used overall-for the primary hash table and all the secondary hash tables-is O(n).
If we store n keys in a hash table of size m = n2 using a hash function h randomly chosen from a universal class of hash functions, then the probability of there being any collisions is less than 1/2.
Proof There are ![]() pairs of keys that may collide; each pair collides with probability 1/m if h is chosen at random from a universal family ℋ of hash functions. Let X be a random variable that counts the number of collisions. When m = n2, the expected number of collisions is
pairs of keys that may collide; each pair collides with probability 1/m if h is chosen at random from a universal family ℋ of hash functions. Let X be a random variable that counts the number of collisions. When m = n2, the expected number of collisions is

(Note that this analysis is similar to the analysis of the birthday paradox in Section 5.4.1.) Applying Markov's inequality (C.29), Pr{X ≥ t} ≤ E[X] /t, with t = 1 completes the proof.
In the situation described in Theorem 11.9, where m = n2, it follows that a hash function h chosen at random from ℋ is more likely than not to have no collisions. Given the set K of n keys to be hashed (remember that K is static), it is thus easy to find a collision-free hash function h with a few random trials.
When n is large, however, a hash table of size m = n2 is excessive. Therefore, we adopt the two-level hashing approach, and we use the approach of Theorem 11.9 only to hash the entries within each slot. An outer, or first-level, hash function h is used to hash the keys into m = n slots. Then, if nj keys hash to slot j, a secondary hash table Sj of size ![]() is used to provide collision-free constant time lookup.
is used to provide collision-free constant time lookup.
We now turn to the issue of ensuring that the overall memory used is O(n). Since the size mj of the jth secondary hash table grows quadratically with the number nj of keys stored, there is a risk that the overall amount of storage could be excessive.
If the first-level table size is m = n, then the amount of memory used is O(n) for the primary hash table, for the storage of the sizes mj of the secondary hash tables, and for the storage of the parameters aj and bj defining the secondary hash functions hj drawn from the class ![]() of Section 11.3.3 (except when nj = 1 and we use a = b = 0). The following theorem and a corollary provide a bound on the expected combined sizes of all the secondary hash tables. A second corollary bounds the probability that the combined size of all the secondary hash tables is superlinear.
of Section 11.3.3 (except when nj = 1 and we use a = b = 0). The following theorem and a corollary provide a bound on the expected combined sizes of all the secondary hash tables. A second corollary bounds the probability that the combined size of all the secondary hash tables is superlinear.
If we store n keys in a hash table of size m = n using a hash function h randomly chosen from a universal class of hash functions, then
where nj is the number of keys hashing to slot j.
Proof We start with the following identity, which holds for any nonnegative integer a:
| (11.6) |
We have
To evaluate the summation ![]() , we observe that it is just the total number of collisions. By the properties of universal hashing, the expected value of this summation is at most
, we observe that it is just the total number of collisions. By the properties of universal hashing, the expected value of this summation is at most
since m = n. Thus,

If we store n keys in a hash table of size m = n using a hash function h randomly chosen from a universal class of hash functions and we set the size of each secondary hash table to ![]() for j = 0, 1, ..., m - 1, then the expected amount of storage required for all secondary hash tables in a perfect hashing scheme is less than 2n.
for j = 0, 1, ..., m - 1, then the expected amount of storage required for all secondary hash tables in a perfect hashing scheme is less than 2n.
Proof Since ![]() for j = 0, 1, ..., m - 1, Theorem 11.10 gives
for j = 0, 1, ..., m - 1, Theorem 11.10 gives
which completes the proof.
If we store n keys in a hash table of size m = n using a hash function h randomly chosen from a universal class of hash functions and we set the size of each secondary hash table to ![]() for j = 0, 1, ..., m - 1, then the probability that the total storage used for secondary hash tables exceeds 4n is less than 1/2.
for j = 0, 1, ..., m - 1, then the probability that the total storage used for secondary hash tables exceeds 4n is less than 1/2.
Proof Again we apply Markov's inequality (C.29), Pr {X ≥ t} ≤ E [X] /t, this time to inequality (11.7), with ![]() and t = 4n:
and t = 4n:

From Corollary 11.12, we see that testing a few randomly chosen hash functions from the universal family will quickly yield one that uses a reasonable amount of storage.
Suppose that we insert n keys into a hash table of size m using open addressing and uniform hashing. Let p(n, m) be the probability that no collisions occur. Show that p(n, m) ≤ e-n(n-1)/2m. (Hint: See equation (3.11).) Argue that when n exceeds ![]() , the probability of avoiding collisions goes rapidly to zero.
, the probability of avoiding collisions goes rapidly to zero.
A hash table of size m is used to store n items, with n ≤ m/2. Open addressing is used for collision resolution.
Assuming uniform hashing, show that for i = 1, 2, ..., n, the probability that the ith insertion requires strictly more than k probes is at most 2-k.
Show that for i = 1, 2, ..., n, the probability that the ith insertion requires more than 2 lg n probes is at most 1/n2.
Let the random variable Xi denote the number of probes required by the ith insertion. You have shown in part (b) that Pr {Xi > 2lg n} ≤ 1/n2. Let the random variable X = max1≤i≤n Xi denote the maximum number of probes required by any of the n insertions.
Show that Pr{X > 2lg n} ≤ 1/n.
Show that the expected length E[X] of the longest probe sequence is O(lg n).
Suppose that we have a hash table with n slots, with collisions resolved by chaining, and suppose that n keys are inserted into the table. Each key is equally likely to be hashed to each slot. Let M be the maximum number of keys in any slot after all the keys have been inserted. Your mission is to prove an O(lg n/lg lg n) upper bound on E[M], the expected value of M.
Argue that the probability Qk that exactly k keys hash to a particular slot is given by
Let Pk be the probability that M = k, that is, the probability that the slot containing the most keys contains k keys. Show that Pk ≤ nQk.
Use Stirling's approximation, equation (3.17), to show that Qk < ek/kk.
Show that there exists a constant c > 1 such that ![]() for k0 = clg n/ lg lg n. Conclude that Pk < 1/n2< for k ≥ k0 = c lg n/ lg lg n.
for k0 = clg n/ lg lg n. Conclude that Pk < 1/n2< for k ≥ k0 = c lg n/ lg lg n.
Argue that
Conclude that E[M] = O(lg n/ lg lg n).
Suppose that we are given a key k to search for in a hash table with positions 0, 1, ..., m - 1, and suppose that we have a hash function h mapping the key space into the set {0, 1, ..., m - 1}. The search scheme is as follows.
Compute the value i ← h(k), and set j ← 0.
Probe in position i for the desired key k. If you find it, or if this position is empty, terminate the search.
Set j ← (j + 1) mod m and i ← (i + j) mod m, and return to step 2.
Assume that m is a power of 2.
Show that this scheme is an instance of the general "quadratic probing" scheme by exhibiting the appropriate constants c1 and c2 for equation (11.5).
Prove that this algorithm examines every table position in the worst case.
Let ℋ = {h} be a class of hash functions in which each h maps the universe U of keys to {0, 1, ..., m - 1}. We say that ℋ is k-universal if, for every fixed sequence of k distinct keys 〈x(1), x(2), ..., x(k)〉 and for any h chosen at random from ℋ, the sequence 〈h(x(1)), h(x(2)), ..., h(x(k))〉 is equally likely to be any of the mk sequences of length k with elements drawn from {0, 1, ..., m - 1}.
Show that if ℋ is 2-universal, then it is universal.
Let U be the set of n-tuples of values drawn from Zp, and let B = Zp, where p is prime. For any n-tuple a = 〈a0, a1, ..., an-1〉 of values from Zp and for any b ∈ Zp, define the hash function ha,b : U → B on an input n-tuple x = 〈x0, x1, ..., xn-1〉 from U as
and let ℋ = {ha,b}. Argue that ℋ is 2-universal.
Suppose that Alice and Bob agree secretly on a hash function ha,b from a 2-universal family ℋ of hash functions. Later, Alice sends a message m to Bob over the Internet, where m ∈ U . She authenticates this message to Bob by also sending an authentication tag t = ha,b(m), and Bob checks that the pair (m, t) he receives satisfies t = ha,b(m). Suppose that an adversary intercepts (m, t) en route and tries to fool Bob by replacing the pair with a different pair (m', t'). Argue that the probability that the adversary succeeds in fooling Bob into accepting (m', t') is at most 1/p, no matter how much computing power the adversary has.
[1]When nj = mj = 1, we don't really need a hash function for slot j; when we Choose a hash function ha,b(k) = ((ak + b) mod p) mod mj for such a slot, we just use a = b = 0.
| < Day Day Up > |