|
|
< Day Day Up > |
|
A binomial heap is a collection of binomial trees, so this section starts by defining binomial trees and proving some key properties. We then define binomial heaps and show how they can be represented.
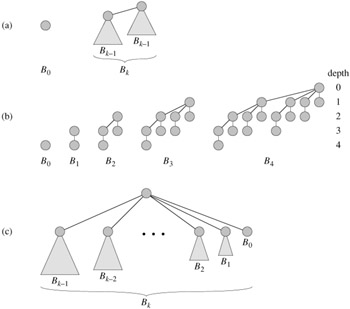
The binomial tree Bk is an ordered tree (see Section B.5.2) defined recursively. As shown in Figure 19.2(a), the binomial tree B0 consists of a single node. The binomial tree Bk consists of two binomial trees Bk-1 that are linked together: the root of one is the leftmost child of the root of the other. Figure 19.2(b) shows the binomial trees B0 through B4.
Some properties of binomial trees are given by the following lemma.
 |
For the binomial tree Bk,
there are 2k nodes,
the height of the tree is k,
there are exactly 
nodes at depth i for i = 0, 1, ..., k, and
the root has degree k, which is greater than that of any other node; moreover if i the children of the root are numbered from left to right by k - 1, k - 2, ..., 0, child i is the root of a subtree Bi.
Proof The proof is by induction on k. For each property, the basis is the binomial tree B0. Verifying that each property holds for B0 is trivial.
For the inductive step, we assume that the lemma holds for Bk-1.
Binomial tree Bk consists of two copies of Bk-1, and so Bk has 2k-1 + 2k-1 = 2k nodes.
Because of the way in which the two copies of Bk-1 are linked to form Bk, the maximum depth of a node in Bk is one greater than the maximum depth in Bk-1. By the inductive hypothesis, this maximum depth is (k - 1) + 1 = k.
Let D(k, i) be the number of nodes at depth i of binomial tree Bk. Since Bk is composed of two copies of Bk-1 linked together, a node at depth i in Bk-1 appears in Bk once at depth i and once at depth i + 1. In other words, the number of nodes at depth i in Bk is the number of nodes at depth i in Bk-1 plus the number of nodes at depth i - 1 in Bk-1. Thus,
The only node with greater degree in Bk than in Bk-1 is the root, which has one more child than in Bk-1. Since the root of Bk-1 has degree k - 1, the root of Bk has degree k. Now, by the inductive hypothesis, and as Figure 19.2(c) shows, from left to right, the children of the root of Bk-1 are roots of Bk-2, Bk-3, ..., B0. When Bk-1 is linked to Bk-1, therefore, the children of the resulting root are roots of Bk-1, Bk-2, ..., B0.
|
|
The maximum degree of any node in an n-node binomial tree is lg n.
Proof Immediate from properties 1 and 4 of Lemma 19.1.
|
The term "binomial tree" comes from property 3 of Lemma 19.1, since the terms 
are the binomial coefficients. Exercise 19.1-3 gives further justification for the term.
A binomial heap H is a set of binomial trees that satisfies the following binomial-heap properties.
Each binomial tree in H obeys the min-heap property: the key of a node is greater than or equal to the key of its parent. We say that each such tree is min-heap-ordered.
For any nonnegative integer k, there is at most one binomial tree in H whose root has degree k.
The first property tells us that the root of a min-heap-ordered tree contains the smallest key in the tree.
The second property implies that an n-node binomial heap H consists of at most ⌊lgn⌋ + 1 binomial trees. To see why, observe that the binary representation of n has ⌊lg n⌋ + 1 bits, say <b⌊lg n⌋, b⌊lg n⌋-1, ..., b0>, so that 
. By property 1 of Lemma 19.1, therefore, binomial tree Bi appears in H if and only if bit bi = 1. Thus, binomial heap H contains at most ⌊lg n⌋ + 1 binomial trees.
Figure 19.3(a) shows a binomial heap H with 13 nodes. The binary representation of 13 is <1101>, and H consists of min-heap-ordered binomial trees B3, B2, and B0, having 8, 4, and 1 nodes respectively, for a total of 13 nodes.
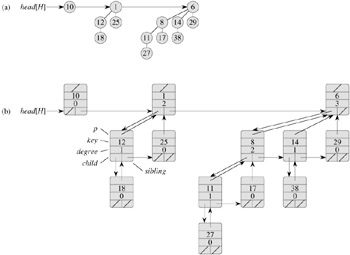
As shown in Figure 19.3(b), each binomial tree within a binomial heap is stored in the left-child, right-sibling representation of Section 10.4. Each node has a key field and any other satellite information required by the application. In addition, each node x contains pointers p[x] to its parent, child[x] to its leftmost child, and sibling[x] to the sibling of x immediately to its right. If node x is a root, then p[x] = NIL. If node x has no children, then child[x] = NIL, and if x is the rightmost child of its parent, then sibling[x] = NIL. Each node x also contains the field degree[x], which is the number of children of x.
As Figure 19.3 also shows, the roots of the binomial trees within a binomial heap are organized in a linked list, which we refer to as the root list. The degrees of the roots strictly increase as we traverse the root list. By the second binomial-heap property, in an n-node binomial heap the degrees of the roots are a subset of {0, 1, ..., ⌊lg n⌋}. The sibling field has a different meaning for roots than for nonroots. If x is a root, then sibling[x] points to the next root in the root list. (As usual, sibling[x] = NIL if x is the last root in the root list.)
A given binomial heap H is accessed by the field head[H], which is simply a pointer to the first root in the root list of H . If binomial heap H has no elements, then head[H] = NIL.
|
Suppose that x is a node in a binomial tree within a binomial heap, and assume that sibling[x] ≠ NIL. If x is not a root, how does degree[sibling[x]] compare to degree[x]? How about if x is a root?
|
|
If x is a nonroot node in a binomial tree within a binomial heap, how does degree[x] compare to degree[p[x]]?
|
|
Suppose we label the nodes of binomial tree Bk in binary by a postorder walk, as in Figure 19.4. Consider a node x labeled l at depth i, and let j = k - i. Show that x has j 1's in its binary representation. How many binary k-strings are there that contain exactly j 1's? Show that the degree of x is equal to the number of 1's to the right of the rightmost 0 in the binary representation of l.
|
|
|
< Day Day Up > |
|
