| < Day Day Up > |
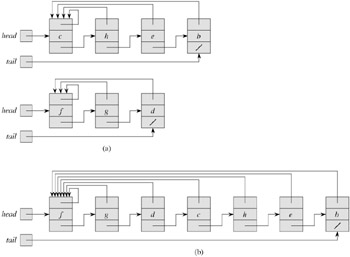
A simple way to implement a disjoint-set data structure is to represent each set by a linked list. The first object in each linked list serves as its set's representative. Each object in the linked list contains a set member, a pointer to the object containing the next set member, and a pointer back to the representative. Each list maintains pointers head, to the representative, and tail, to the last object in the list. Figure 21.2(a) shows two sets. Within each linked list, the objects may appear in any order (subject to our assumption that the first object in each list is the representative).
With this linked-list representation, both MAKE-SET and FIND-SET are easy, requiring O(1) time. To carry out MAKE-SET(x), we create a new linked list whose only object is x. For FIND-SET(x), we just return the pointer from x back to the representative.
The simplest implementation of the UNION operation using the linked-list set representation takes significantly more time than MAKE-SET or FIND-SET. As Figure 21.2(b) shows, we perform UNION(x, y) by appending x's list onto the end of y's list. We use the tail pointer for y's list to quickly find where to append x's list. The representative of the new set is the element that was originally the representative of the set containing y. Unfortunately, we must update the pointer to the representative for each object originally on x's list, which takes time linear in the length of x's list.
In fact, it is not difficult to come up with a sequence of m operations on n objects that requires Θ(n2) time. Suppose that we have objects x1, x2, ..., xn. We execute the sequence of n MAKE-SET operations followed by n - 1 UNION operations shown in Figure 21.3, so that m = 2n - 1. We spend Θ(n) time performing the n MAKE-SET operations. Because the ith UNION operation updates i objects, the total number of objects updated by all n - 1 UNION operations is
|
Operation |
Number of objects updated |
|---|---|
|
|
|
|
MAKE-SET(x1) |
1 |
|
MAKE-SET(x2) |
1 |
|
⋮ |
⋮ |
|
MAKE-SET(xn |
1 |
|
UNION(x1, x2) |
1 |
|
UNION(x2, x3) |
2 |
|
UNION(x3, x4) |
3 |
|
⋮ |
⋮ |
|
UNION(xn-1, xn) |
n - 1 |
The total number of operations is 2n - 1, and so each operation on average requires Θ(n) time. That is, the amortized time of an operation is Θ(n).
In the worst case, the above implementation of the UNION procedure requires an average of Θ(n) time per call because we may be appending a longer list onto a shorter list; we must update the pointer to the representative for each member of the longer list. Suppose instead that each list also includes the length of the list (which is easily maintained) and that we always append the smaller list onto the longer, with ties broken arbitrarily. With this simple weighted-union heuristic, a single UNION operation can still take Ω(n) time if both sets have Ω(n) members. As the following theorem shows, however, a sequence of m MAKE-SET, UNION, and FIND-SET operations, n of which are MAKE-SET operations, takes O(m + n lg n) time.
Using the linked-list representation of disjoint sets and the weighted-union heuristic, a sequence of m MAKE-SET, UNION, and FIND-SET operations, n of which are MAKE-SET operations, takes O(m + n lg n) time.
Proof We start by computing, for each object in a set of size n, an upper bound on the number of times the object's pointer back to the representative has been updated. Consider a fixed object x. We know that each time x's representative pointer was updated, x must have started in the smaller set. The first time x's representative pointer was updated, therefore, the resulting set must have had at least 2 members. Similarly, the next time x's representative pointer was updated, the resulting set must have had at least 4 members. Continuing on, we observe that for any k ≤ n, after x's representative pointer has been updated ⌈lg k⌉ times, the resulting set must have at least k members. Since the largest set has at most n members, each object's representative pointer has been updated at most ⌈lg n⌉ times over all the UNION operations. We must also account for updating the head and tail pointers and the list lengths, which take only Θ(1) time per UNION operation. The total time used in updating the n objects is thus O(n lg n).
The time for the entire sequence of m operations follows easily. Each MAKE-SET and FIND-SET operation takes O(1) time, and there are O(m) of them. The total time for the entire sequence is thus O(m + n lg n).
Write pseudocode for MAKE-SET, FIND-SET, and UNION using the linked-list representation and the weighted-union heuristic. Assume that each object x has an attribute rep[x] pointing to the representative of the set containing x and that each set S has attributes head[S], tail[S], and size[S] (which equals the length of the list).
Show the data structure that results and the answers returned by the FIND-SET operations in the following program. Use the linked-list representation with the weighted-union heuristic.
1 for i ← 1 to 16 2 do MAKE-SET(xi) 3 for i ← 1 to 15 by 2 4 do UNION(xi, xi+1) 5 for i ← 1 to 13 by 4 6 do UNION(xi, xi+2) 7 UNION(x1, x5) 8 UNION(x11, x13) 9 UNION(x1, x10) 10 FIND-SET(x2) 11 FIND-SET(x9)
Assume that if the sets containing xi and xj have the same size, then the operation UNION(xi, xj) appends xj's list onto xi's list.
Adapt the aggregate proof of Theorem 21.1 to obtain amortized time bounds of O(1) for MAKE-SET and FIND-SET and O(lg n) for UNION using the linked-list representation and the weighted-union heuristic.
Give a tight asymptotic bound on the running time of the sequence of operations in Figure 21.3 assuming the linked-list representation and the weighted-union heuristic.
Suggest a simple change to the UNION procedure for the linked-list representation that removes the need to keep the tail pointer to the last object in each list. Whether or not the weighted-union heuristic is used, your change should not change the asymptotic running time of the UNION procedure. (Hint: Rather than appending one list to another, splice them together.)
| < Day Day Up > |