Relaxation

The algorithms in this chapter use the technique of relaxation. For each vertex v ∈ V, we maintain an attribute d[v], which is an upper bound on the weight of a shortest path from source s to v. We call d[v] a shortest-path estimate. We initialize the shortest-path estimates and predecessors by the following Θ(V)-time procedure.

INITIALIZE-SINGLE-SOURCE(G, s)
1  for each vertex v ∈ V[G]
2       do d[v] ← ∞
3          π[v] ← NIL
4  d[s] 0

After initialization, π[v] = NIL for all v ∈ V, d[s] = 0, and d[v] = ∞ for v ∈ V - {s}.

The process of relaxing^[1] an edge (u, v) consists of testing whether we can improve the shortest path to v found so far by going through u and, if so, updating d[v] and π[v]. A relaxation step may decrease the value of the shortest-path esti-mate d[v] and update v's predecessor field π[v]. The following code performs a relaxation step on edge (u, v).

RELAX(u, v, w)
1  if d[v] > d[u] + w(u, v)
2     then d[v] ← d[u] + w(u, v)
3          π[v] ← u

Figure 24.3 shows two examples of relaxing an edge, one in which a shortest-path estimate decreases and one in which no estimate changes.

Figure 24.3: Relaxation of an edge (u, v) with weight w(u, v) = 2. The shortest-path estimate of each vertex is shown within the vertex. (a) Because d[v] > d[u] + w(u, v) prior to relaxation, the value of d[v] decreases. (b) Here, d[v] ≤ d[u] + w(u, v) before the relaxation step, and so d[v] is unchanged by relaxation.

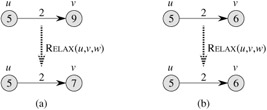
Each algorithm in this chapter calls INITIALIZE-SINGLE-SOURCE and then repeatedly relaxes edges. Moreover, relaxation is the only means by which shortestpath estimates and predecessors change. The algorithms in this chapter differ in how many times they relax each edge and the order in which they relax edges. In Dijkstra's algorithm and the shortest-paths algorithm for directed acyclic graphs, each edge is relaxed exactly once. In the Bellman-Ford algorithm, each edge is relaxed many times.