| < Day Day Up > |
We now have all the necessary tools to construct a network that can sort any input sequence. The sorting network SORTER[n] uses the merging network to implement a parallel version of merge sort from Section 2.3.1. The construction and operation of the sorting network are illustrated in Figure 27.12.
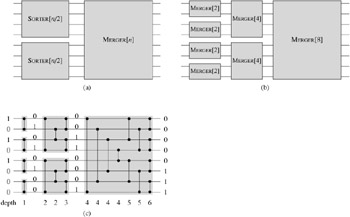
Figure 27.12(a) shows the recursive construction of SORTER[n]. The n input elements are sorted by using two copies of SORTER[n/2] recursively to sort (in parallel) two subsequences of length n/2 each. The two resulting sequences are then merged by MERGER[n]. The boundary case for the recursion is when n = 1, in which case we can use a wire to sort the 1-element sequence, since a 1-element sequence is already sorted. Figure 27.12(b) shows the result of unrolling the recursion, and Figure 27.12(c) shows the actual network obtained by replacing the MERGER boxes in Figure 27.12(b) with the actual merging networks.
Data pass through lg n stages in the network SORTER[n]. Each of the individual inputs to the network is already a sorted 1-element sequence. The first stage of SORTER[n] consists of n/2 copies of MERGER[2] that work in parallel to merge pairs of 1-element sequences to produce sorted sequences of length 2. The second stage consists of n/4 copies of MERGER[4] that merge pairs of these 2-element sorted sequences to produce sorted sequences of length 4. In general, for k = 1, 2,..., lg n, stage k consists of n/2k copies of MERGER[2k] that merge pairs of the 2k-1-element sorted sequences to produce sorted sequences of length 2k. At the final stage, one sorted sequence consisting of all the input values is produced. This sorting network can be shown by induction to sort zero-one sequences, and consequently, by the zero-one principle (Theorem 27.2), it can sort arbitrary values.
We can analyze the depth of the sorting network recursively. The depth D(n) of SORTER[n] is the depth D(n/2) of SORTER[n/2] (there are two copies of SORTER[n/2], but they operate in parallel) plus the depth lg n of MERGER[n]. Consequently, the depth of SORTER[n] is given by the recurrence
whose solution is D(n) = Θ(lg2 n). (Use the version of the master method given in Exercise 4.4-2.) Thus, we can sort n numbers in parallel in O(lg2 n) time.
Suppose that we have 2n elements 〈a1, a2,..., a2n〉 and wish to partition them into the n smallest and the n largest. Prove that we can do this in constant additional depth after separately sorting 〈a1, a2,..., an〉 and 〈an+1, an+2,..., a2n〉.
Let S(k) be the depth of a sorting network with k inputs, and let M(k) be the depth of a merging network with 2k inputs. Suppose that we have a sequence of n numbers to be sorted and we know that every number is within k positions of its correct position in the sorted order. Show that we can sort the n numbers in depth S(k) + 2M(k).
We can sort the entries of an m × m matrix by repeating the following procedure k times:
Sort each odd-numbered row into monotonically increasing order.
Sort each even-numbered row into monotonically decreasing order.
Sort each column into monotonically increasing order.
How many iterations k are required for this procedure to sort, and in what order should we read the matrix entries after the k iterations to obtain the sorted output?
A comparison network is a transposition network if each comparator connects adjacent lines, as in the network in Figure 27.3.
Show that any transposition sorting network with n inputs has Ω(n2) comparators.
Prove that a transposition network with n inputs is a sorting network if and only if it sorts the sequence 〈n, n - 1,..., 1〉. (Hint: Use an induction argument analogous to the one in the proof of Lemma 27.1.)
An odd-even sorting network on n inputs 〈a1,a2,...,an〉 is a transposition sorting network with n levels of comparators connected in the "brick-like" pattern illustrated in Figure 27.13. As can be seen in the figure, for i = 1, 2,..., n and d = 1, 2,..., n, line i is connected by a depth-d comparator to line j = i + (-1)i+d if 1 ≤ j ≤ n.
Prove that odd-even sorting networks actually sort.
In Section 27.4, we saw how to construct a merging network based on bitonic sorting. In this problem, we shall construct an odd-even merging network. We assume that n is an exact power of 2, and we wish to merge the sorted sequence of elements on lines 〈a1, a2,..., an〉 with those on lines 〈an+1, an+2,..., a2n〉. If n = 1, we put a comparator between lines a1 and a2. Otherwise, we recursively construct two odd-even merging networks that operate in parallel. The first merges the sequence on lines 〈a1, a3,..., an-1〉 with the sequence on lines 〈an+1, an+3,..., a2n-1〉 (the odd elements). The second merges 〈a2, a4,..., an〉 with 〈an+2, an+4,..., a2n〉 (the even elements). To combine the two sorted subsequences, we put a comparator between a2i and a2i + 1 for i = 1, 2,..., n - 1.
Draw a 2n-input merging network for n = 4.
Professor Corrigan suggests that to combine the two sorted subsequences produced by the recursive merging, instead of putting a comparator between a2i and a2i+1 for i = 1, 2,..., n - 1, one should put a comparator between a2i-1 and a2i for i = 1, 2,..., n. Draw such a 2n-input network for n = 4, and give a counterexample to show that the professor is mistaken in thinking that the network produced is a merging network. Show that the 2n-input merging network from part (a) works properly on your example.
Use the zero-one principle to prove that any 2n-input odd-even merging network is indeed a merging network.
What is the depth of a 2n-input odd-even merging network? What is its size?
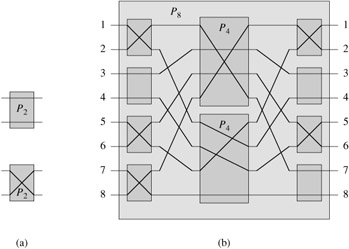
A permutation network on n inputs and n outputs has switches that allow it to connect its inputs to its outputs according to any of the n! possible permutations. Figure 27.14(a) shows the 2-input, 2-output permutation network P2, which consists of a single switch that can be set either to feed its inputs straight through to its outputs or to cross them.
Argue that if we replace each comparator in a sorting network with the switch of Figure 27.14(a), the resulting network is a permutation network. That is, for any permutation π, there is a way to set the switches in the network so that input i is connected to output π(i).
Figure 27.14(b) shows the recursive construction of an 8-input, 8-output permutation network P8 that uses two copies of P4 and 8 switches. The switches have been set to realize the permutation π = 〈π(1), π(2),..., π(8)〉 = 〈4, 7, 3, 5, 1, 6, 8, 2〉, which requires (recursively) that the top P4 realize 〈4, 2, 3, 1〉 and the bottom P4 realize 〈2, 3, 1, 4〉.
Show how to realize the permutation 〈5, 3, 4, 6, 1, 8, 2, 7〉 on P8 by drawing the switch settings and the permutations performed by the two P4's.
Let n be an exact power of 2. Define Pn recursively in terms of two Pn/2's in a manner similar to the way we defined P8.
Describe an O(n)-time (ordinary random-access machine) algorithm that sets the n switches connected to the inputs and outputs of Pn and specifies the permutations that must be realized by each Pn/2 in order to accomplish any given n-element permutation. Prove that your algorithm is correct.
What are the depth and size of Pn? How long does it take on an ordinary random-access machine to compute all switch settings, including those within the Pn/2's?
Argue that for n > 2, any permutation network-not just Pn-must realize some permutation by two distinct combinations of switch settings.
| < Day Day Up > |