Coefficient representation

A coefficient representation of a polynomial of degree-bound n is a vector of coefficients a = (a₀, a₁,..., a_n-1). In matrix equations in this chapter, we shall generally treat vectors as column vectors.

The coefficient representation is convenient for certain operations on polynomials. For example, the operation of evaluating the polynomial A(x) at a given point x₀ consists of computing the value of A(x₀). Evaluation takes time Θ(n) using Horner's rule:

A(x₀) = a₀ + x₀(a₁ + x₀(a₂ + ··· + x₀(a_n-2 + x₀(a_n-1)) )).

Similarly, adding two polynomials represented by the coefficient vectors a = (a₀, a₁,..., a_n-1) and b = (b₀, b₁,..., b_n-1) takes Θ(n) time: we just produce the coefficient vector c = (c₀, c₁,..., c_n-1), where c_j = a_j + b_j for j = 0, 1,..., n - 1.

Now, consider the multiplication of two degree-bound n polynomials A(x) and B(x) represented in coefficient form. If we use the method described by equations (30.1) and (30.2), polynomial multiplication takes time Θ(n²), since each coefficient in the vector a must be multiplied by each coefficient in the vector b. The operation of multiplying polynomials in coefficient form seems to be considerably more difficult than that of evaluating a polynomial or adding two polynomials. The resulting coefficient vector c, given by equation (30.2), is also called the convolution of the input vectors a and b, denoted c = a ⊗ b. Since multiplying polynomials and computing convolutions are fundamental computational problems of considerable practical importance, this chapter concentrates on efficient algorithms for them.

Point-value representation

A point-value representation of a polynomial A(x) of degree-bound n is a set of n point-value pairs

{(x₀, y₀), (x₁, y₁),..., (x_n-1, y_n-1)}

such that all of the x_k are distinct and

for k = 0, 1,.., n - 1. A polynomial has many different point-value representations, since any set of n distinct points x₀, x₁,..., x_n-1 can be used as a basis for the representation.

Computing a point-value representation for a polynomial given in coefficient form is in principle straightforward, since all we have to do is select n distinct points x₀, x₁,..., x_n-1 and then evaluate A(x_k) for k = 0, 1,..., n - 1. With Horner's method, this n-point evaluation takes time Θ(n²). We shall see later that if we choose the x_k cleverly, this computation can be accelerated to run in time Θ(n lg n).

The inverse of evaluation -determining the coefficient form of a polynomial from a point-value representation -is called interpolation. The following theorem shows that interpolation is well defined, assuming that the degree-bound of the interpolating polynomial equals the number of given point-value pairs.

The proof of Theorem 30.1 describes an algorithm for interpolation based on solving the set (30.4) of linear equations. Using the LU decomposition algorithms of Chapter 28, we can solve these equations in time O(n³).

A faster algorithm for n-point interpolation is based on Lagrange's formula:

You may wish to verify that the right-hand side of equation (30.5) is a polynomial of degree-bound n that satisfies A(x_i) = y_i for all i. Exercise 30.1-5 asks you how to compute the coefficients of A using Lagrange's formula in time Θ(n²).

Thus, n-point evaluation and interpolation are well-defined inverse operations that transform between the coefficient representation of a polynomial and a point-value representation.^[1] The algorithms described above for these problems take time Θ(n²).

The point-value representation is quite convenient for many operations on polynomials. For addition, if C(x) = A(x) + B(x), then C(x_k) = A(x_k) + B(x_k) for any point x_k. More precisely, if we have a point-value representation for A,

{(x₀, y₀), (x₁, y₁),..., (x_n-1, y_n-1)},

and for B,

(note that A and B are evaluated at the same n points), then a point-value representation for C is

Thus, the time to add two polynomials of degree-bound n in point-value form is Θ(n).

Similarly, the point-value representation is convenient for multiplying polynomials. If C(x) = A(x) B(x), then C(x_k) = A(x_k)B(x_k) for any point x_k, and we can pointwise multiply a point-value representation for A by a point-value representation for B to obtain a point-value representation for C. We must face the problem, however, that the degree-bound of C is the sum of the degree-bounds for A and B. A standard point-value representation for A and B consists of n point-value pairs for each polynomial. Multiplying these together gives us n point-value pairs for C, but since the degree-bound of C is 2n, we need 2n point-value pairs for a point-value representation of C. (See Exercise 30.1-4.) We must therefore begin with "extended" point-value representations for A and for B consisting of 2n point-value pairs each. Given an extended point-value representation for A,

{(x₀,y₀),(x₁,y₁),...,(x_2n-1,y_2n-1)},

and a corresponding extended point-value representation for B,

then a point-value representation for C is

Given two input polynomials in extended point-value form, we see that the time to multiply them to obtain the point-value form of the result is Θ(n), much less than the time required to multiply polynomials in coefficient form.

Finally, we consider how to evaluate a polynomial given in point-value form at a new point. For this problem, there is apparently no approach that is simpler than converting the polynomial to coefficient form first, and then evaluating it at the new point.

Fast multiplication of polynomials in coefficient form

Can we use the linear-time multiplication method for polynomials in point-value form to expedite polynomial multiplication in coefficient form? The answer hinges on our ability to convert a polynomial quickly from coefficient form to point-value form (evaluate) and vice-versa (interpolate).

We can use any points we want as evaluation points, but by choosing the evaluation points carefully, we can convert between representations in only Θ(n lg n) time. As we shall see in Section 30.2, if we choose "complex roots of unity" as the evaluation points, we can produce a point-value representation by taking the Discrete Fourier Transform (or DFT) of a coefficient vector. The inverse operation, interpolation, can be performed by taking the "inverse DFT" of point-value pairs, yielding a coefficient vector. Section 30.2 will show how the FFT performs the DFT and inverse DFT operations in Θ(n lg n) time.

Figure 30.1 shows this strategy graphically. One minor detail concerns degree-bounds. The product of two polynomials of degree-bound n is a polynomial of degree-bound 2n. Before evaluating the input polynomials A and B, therefore, we first double their degree-bounds to 2n by adding n high-order coefficients of 0. Because the vectors have 2n elements, we use "complex (2n)th roots of unity," which are denoted by the w_2n terms in Figure 30.1.

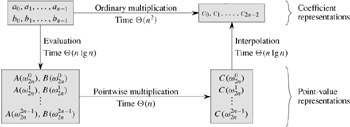
Given the FFT, we have the following Θ(n lg n)-time procedure for multiplying two polynomials A(x) and B(x) of degree-bound n, where the input and output representations are in coefficient form. We assume that n is a power of 2; this requirement can always be met by adding high-order zero coefficients.

1. Double degree-bound: Create coefficient representations of A(x) and B(x) as degree-bound 2n polynomials by adding n high-order zero coefficients to each.

2. Evaluate: Compute point-value representations of A(x) and B(x) of length 2n through two applications of the FFT of order 2n. These representations contain the values of the two polynomials at the (2n)th roots of unity.

3. Pointwise multiply: Compute a point-value representation for the polynomial C(x) = A(x)B(x) by multiplying these values together pointwise. This representation contains the value of C(x) at each (2n)th root of unity.

4. Interpolate: Create the coefficient representation of the polynomial C(x) through a single application of an FFT on 2n point-value pairs to compute the inverse DFT.

Steps (1) and (3) take time Θ(n), and steps (2) and (4) take time Θ(n lg n). Thus, once we show how to use the FFT, we will have proven the following.