Pollard's rho heuristic

Trial division by all integers up to B is guaranteed to factor completely any number up to B². For the same amount of work, the following procedure will factor any number up to B⁴ (unless we're unlucky). Since the procedure is only a heuristic, neither its running time nor its success is guaranteed, although the procedure is very effective in practice. Another advantage of the POLLARD-RHO procedure is that it uses only a constant number of memory locations. (You can easily implement Pollard-Rho on a programmable pocket calculator to find factors of small numbers.)

POLLARD-RHO(n)
 1  i ← 1
 2  x1 ← RANDOM(0, n - 1)
 3  y ← x1
 4  k ← 2
 5  while TRUE
 6      do i ← i + 1
 7          mod n
 8         d ← gcd(y - xi, n)
 9         if d ≠ 1 and d ≠ n
10            then print d
11         if i = k
12            then y ← xi
13                 k ← 2k

The procedure works as follows. Lines 1-2 initialize i to 1 and x₁ to a randomly chosen value in Z_n. The while loop beginning on line 5 iterates forever, searching for factors of n. During each iteration of the while loop, the recurrence

(31.41)

is used on line 7 to produce the next value of x_i in the infinite sequence

(31.42)

the value of i is correspondingly incremented on line 6. The code is written using subscripted variables x_i for clarity, but the program works the same if all of the subscripts are dropped, since only the most recent value of x_i need be maintained. With this modification, the procedure uses only a constant number of memory locations.

Every so often, the program saves the most recently generated x_i value in the variable y. Specifically, the values that are saved are the ones whose subscripts are powers of 2:

x₁, x₂, x₄, x₈, x₁₆, .... .

Line 3 saves the value x₁, and line 12 saves x_k whenever i is equal to k. The variable k is initialized to 2 in line 4, and k is doubled in line 13 whenever y is updated. Therefore, k follows the sequence 1, 2, 4, 8, ... and always gives the subscript of the next value x_k to be saved in y.

Lines 8-10 try to find a factor of n, using the saved value of y and the current value of x_i . Specifically, line 8 computes the greatest common divisor d = gcd(y - x_i, n). If d is a nontrivial divisor of n (checked in line 9), then line 10 prints d.

This procedure for finding a factor may seem somewhat mysterious at first. Note, however, that POLLARD-RHO never prints an incorrect answer; any number it prints is a nontrivial divisor of n. POLLARD-RHO may not print anything at all, though; there is no guarantee that it will produce any results. We shall see, however, that there is good reason to expect POLLARD-RHO to print a factor p of n after iterations of the while loop. Thus, if n is composite, we can expect this procedure to discover enough divisors to factor n completely after approximately n^1/4 updates, since every prime factor p of n except possibly the largest one is less than .

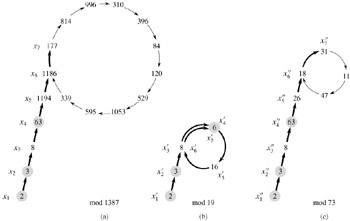
We begin our analysis of the behavior of this procedure by studying how long it takes a random sequence modulo n to repeat a value. Since Z_n is finite, and since each value in the sequence (31.42) depends only on the previous value, the sequence (31.42) eventually repeats itself. Once we reach an x_i such that x_i = x_j for some j < i, we are in a cycle, since x_i+1 = x_j+1, x_i+2 = x_j+2, and so on. The reason for the name "rho heuristic" is that, as Figure 31.7 shows, the sequence x₁, x₂, ..., x_j-1 can be drawn as the "tail" of the rho, and the cycle x_j, x_j+1, ..., x_i as the "body" of the rho.

Figure 31.7: Pollard's rho heuristic. (a) The values produced by the recurrence mod 1387, starting with x₁ = 2. The prime factorization of 1387 is 19 · 73. The heavy arrows indicate the iteration steps that are executed before the factor 19 is discovered. The light arrows point to unreached values in the iteration, to illustrate the "rho" shape. The shaded values are the y values stored by POLLARD-RHO. The factor 19 is discovered upon reaching x₇ = 177, when gcd(63 - 177, 1387) = 19 is computed. The first x value that would be repeated is 1186, but the factor 19 is discovered before this value is repeated. (b) The values produced by the same recurrence, modulo 19. Every value x_i given in part (a) is equivalent, modulo 19, to the value shown here. For example, both x₄ = 63 and x₇ = 177 are equivalent to 6, modulo 19. (c) The values produced by the same recurrence, modulo 73. Every value x_i given in part (a) is equivalent, modulo 73, to the value shown here. By the Chinese remainder theorem, each node in part (a) corresponds to a pair of nodes, one from part (b) and one from part (c).

Let us consider the question of how long it takes for the sequence of x_i to repeat. This is not exactly what we need, but we shall then see how to modify the argument.

For the purpose of this estimation, let us assume that the function

f_n(x) = (x² - 1) mod n

behaves like a "random" function. Of course, it is not really random, but this assumption yields results consistent with the observed behavior of POLLARD-RHO. We can then consider each x_i to have been independently drawn from Z_n according to a uniform distribution on Z_n. By the birthday-paradox analysis of Section 5.4.1, the expected number of steps taken before the sequence cycles is .

Now for the required modification. Let p be a nontrivial factor of n such that gcd(p, n/p) = 1. For example, if n has the factorization , then we may take p to be . (If e₁ = 1, then p is just the smallest prime factor of n, a good example to keep in mind.)

The sequence 〈x_i〉 induces a corresponding sequence modulo p, where

mod p

for all i.

Furthermore, because f_n is defined using only arithmetic operations (squaring and subtraction) modulo n, we shall see that one can compute from the "modulo p" view of the sequence is a smaller version of what is happening modulo n:

Thus, although we are not explicitly computing the sequence , this sequence is well defined and obeys the same recurrence as the sequence 〈x_i〉.

Reasoning as before, we find that the expected number of steps before the sequence repeats is . If p is small compared to n, the sequence may repeat much more quickly than the sequence 〈x_i〉. Indeed, the sequence repeats as soon as two elements of the sequence 〈x_i〉 are merely equivalent modulo p, rather than equivalent modulo n. See Figure 31.7, parts (b) and (c), for an illustration.

Let t denote the index of the first repeated value in the sequence, and let u > 0 denote the length of the cycle that has been thereby produced. That is, t and u > 0 are the smallest values such that for all i ≥ 0. By the above arguments, the expected values of t and u are both . Note that if , then p |(x_t+u+i - x_t+i). Thus, gcd(x_t+u+i - x_t+i, n) > 1.

Therefore, once POLLARD-RHO has saved as y any value x_k such that k ≥ t, then y mod p is always on the cycle modulo p. (If a new value is saved as y, that value is also on the cycle modulo p.) Eventually, k is set to a value that is greater than u, and the procedure then makes an entire loop around the cycle modulo p without changing the value of y. A factor of n is then discovered when x_i "runs into" the previously stored value of y, modulo p, that is, when x_i ≢ y (mod p).

Presumably, the factor found is the factor p, although it may occasionally happen that a multiple of p is discovered. Since the expected values of both t and u are , the expected number of steps required to produce the factor p is .

There are two reasons why this algorithm may not perform quite as expected. First, the heuristic analysis of the running time is not rigorous, and it is possible that the cycle of values, modulo p, could be much larger than . In this case, the algorithm performs correctly but much more slowly than desired. In practice, this issue seems to be moot. Second, the divisors of n produced by this algorithm might always be one of the trivial factors 1 or n. For example, suppose that n = pq, where p and q are prime. It can happen that the values of t and u for p are identical with the values of t and u for q, and thus the factor p is always revealed in the same gcd operation that reveals the factor q. Since both factors are revealed at the same time, the trivial factor pq = n is revealed, which is useless. Again, this problem seems to be insignificant in practice. If necessary, the heuristic can be restarted with a different recurrence of the form mod n. (The values c = 0 and c = 2 should be avoided for reasons we won't go into here, but other values are fine.)

Of course, this analysis is heuristic and not rigorous, since the recurrence is not really "random." Nonetheless, the procedure performs well in practice, and it seems to be as efficient as this heuristic analysis indicates. It is the method of choice for finding small prime factors of a large number. To factor a β-bit composite number n completely, we only need to find all prime factors less than ⌊n^1/2⌋, and so we expect POLLARD-RHO to require at most n^1/4 = 2^β/4 arithmetic operations and at most n^1/4β² = 2^β/4β² bit operations. POLLARD-RHO's ability to find a small factor p of n with an expected number of arithmetic operations is often its most appealing feature.

Exercises 31.9-1

Referring to the execution history shown in Figure 31.7(a), when does POLLARD-RHO print the factor 73 of 1387?

Exercises 31.9-2

Suppose that we are given a function f : Z_n ∈ Z_n and an initial value x₀ ∈ Z_n. Define x_i = f (x_i-1) for i = 1, 2, .... Let t and u > 0 be the smallest values such that x_t+i = x_t+u+i for i = 0, 1, .... In the terminology of Pollard's rho algorithm, t is the length of the tail and u is the length of the cycle of the rho. Give an efficient algorithm to determine t and u exactly, and analyze its running time.

Exercises 31.9-3

How many steps would you expect POLLARD-RHO to require to discover a factor of the form p^e, where p is prime and e > 1?

Exercises 31.9-4: ★

One disadvantage of POLLARD-RHO as written is that it requires one gcd computation for each step of the recurrence. It has been suggested that we might batch the gcd computations by accumulating the product of several x_i values in a row and then using this product instead of x_i in the gcd computation. Describe carefully how you would implement this idea, why it works, and what batch size you would pick as the most effective when working on a β-bit number n.

Problems 31-1: Binary gcd algorithm

On most computers, the operations of subtraction, testing the parity (odd or even) of a binary integer, and halving can be performed more quickly than computing remainders. This problem investigates the binary gcd algorithm, which avoids the remainder computations used in Euclid's algorithm.

1. Prove that if a and b are both even, then gcd(a, b) = 2 gcda/2, b/2).

2. Prove that if a is odd and b is even, then gcd(a, b) = gcd(a, b/2).

3. Prove that if a and b are both odd, then gcd(a, b) = gcd((a - b)/2, b).

4. Design an efficient binary gcd algorithm for input integers a and b, where a ≥ b, that runs in O(lg a) time. Assume that each subtraction, parity test, and halving can be performed in unit time.

Problems 31-2: Analysis of bit operations in Euclid's algorithm

1. Consider the ordinary "paper and pencil" algorithm for long division: dividing a by b, which yields a quotient q and remainder r. Show that this method requires O((1 + lg q) lg b) bit operations.

2. Define μ(a, b) = (1 + lg a)(1 + lg b). Show that the number of bit operations performed by EUCLID in reducing the problem of computing gcd(a, b) to that of computing gcd(b, a mod b) is at most c(μ(a, b) - μ(b, a mod b)) for some sufficiently large constant c > 0.

3. Show that EUCLID(a, b) requires O(μ(a, b)) bit operations in general and O(β²) bit operations when applied to two β-bit inputs.

Exercises 31-3: Three algorithms for Fibonacci numbers

This problem compares the efficiency of three methods for computing the nth Fibonacci number F_n, given n. Assume that the cost of adding, subtracting, or multiplying two numbers is O(1), independent of the size of the numbers.

1. Show that the running time of the straightforward recursive method for computing F_n based on recurrence (3.21) is exponential in n.

2. Show how to compute F_n in O(n) time using memoization.

3. Show how to compute F_n in O(lg n) time using only integer addition and multiplication. (Hint: Consider the matrix

   

   and its powers.)

4. Assume now that adding two β-bit numbers takes Θ(β) time and that multiplying two β-bit numbers takes Θ(β²) time. What is the running time of these three methods under this more reasonable cost measure for the elementary arithmetic operations?

Problems 31-4: Quadratic residues

Let p be an odd prime. A number is a quadratic residue if the equation x² = a (mod p) has a solution for the unknown x.

1. Show that there are exactly (p - 1)/2 quadratic residues, modulo p.

2. If p is prime, we define the Legendre symbol , for , to be 1 if a is a quadratic residue modulo p and -1 otherwise. Prove that if , then

   

   Give an efficient algorithm for determining whether or not a given number a is a quadratic residue modulo p. Analyze the efficiency of your algorithm.

3. Prove that if p is a prime of the form 4k + 3 and a is a quadratic residue in , then a^k+1 mod p is a square root of a, modulo p. How much time is required to find the square root of a quadratic residue a modulo p?

4. Describe an efficient randomized algorithm for finding a nonquadratic residue, modulo an arbitrary prime p, that is, a member of that is not a quadratic residue. How many arithmetic operations does your algorithm require on average?