| < Day Day Up > |
This section presents an algorithm for determining whether any two line segments in a set of segments intersect. The algorithm uses a technique known as "sweeping," which is common to many computational-geometry algorithms. Moreover, as the exercises at the end of this section show, this algorithm, or simple variations of it, can be used to solve other computational-geometry problems.
The algorithm runs in O(n lg n) time, where n is the number of segments we are given. It determines only whether or not any intersection exists; it does not print all the intersections. (By Exercise 33.2-1, it takes Ω(n2) time in the worst case to find all the intersections in a set of n line segments.)
In sweeping, an imaginary vertical sweep line passes through the given set of geometric objects, usually from left to right. The spatial dimension that the sweep line moves across, in this case the x-dimension, is treated as a dimension of time. Sweeping provides a method for ordering geometric objects, usually by placing them into a dynamic data structure, and for taking advantage of relationships among them. The line-segment-intersection algorithm in this section considers all the line-segment endpoints in left-to-right order and checks for an intersection each time it encounters an endpoint.
To describe and prove correct our algorithm for determining whether any two of n line segments intersect, we shall make two simplifying assumptions. First, we assume that no input segment is vertical. Second, we assume that no three input segments intersect at a single point. Exercises 33.2-8 and 33.2-9 ask you to show that the algorithm is robust enough that it needs only a slight modification to work even when these assumptions do not hold. Indeed, removing such simplifying assumptions and dealing with boundary conditions is often the most difficult part of programming computational-geometry algorithms and proving their correctness.
Since we assume that there are no vertical segments, any input segment that intersects a given vertical sweep line intersects it at a single point. Thus, we can order the segments that intersect a vertical sweep line according to the y-coordinates of the points of intersection.
To be more precise, consider two segments s1 and s2. We say that these segments are comparable at x if the vertical sweep line with x-coordinate x intersects both of them. We say that s1 is above s2 at x, written s1 >x s2, if s1 and s2 are comparable at x and the intersection of s1 with the sweep line at x is higher than the intersection of s2 with the same sweep line. In Figure 33.4(a), for example, we have the relationships a >r c, a >t b, b >t c, a >t c, and b >u c. Segment d is not comparable with any other segment.
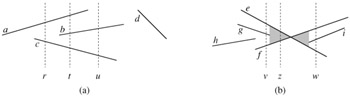
For any given x, the relation ">x" is a total order (see Section B.2) on segments that intersect the sweep line at x. The order may differ for differing values of x, however, as segments enter and leave the ordering. A segment enters the ordering when its left endpoint is encountered by the sweep, and it leaves the ordering when its right endpoint is encountered.
What happens when the sweep line passes through the intersection of two segments? As Figure 33.4(b) shows, their positions in the total order are reversed. Sweep lines v and w are to the left and right, respectively, of the point of intersection of segments e and f, and we have e >v f and f >w e. Note that because we assume that no three segments intersect at the same point, there must be some vertical sweep line x for which intersecting segments e and f are consecutive in the total order >x. Any sweep line that passes through the shaded region of Figure 33.4(b), such as z, has e and f consecutive in its total order.
Sweeping algorithms typically manage two sets of data:
The sweep-line status gives the relationships among the objects intersected by the sweep line.
The event-point schedule is a sequence of x-coordinates, ordered from left to right, that defines the halting positions of the sweep line. We call each such halting position an event point. Changes to the sweep-line status occur only at event points.
For some algorithms (the algorithm asked for in Exercise 33.2-7, for example), the event-point schedule is determined dynamically as the algorithm progresses. The algorithm at hand, however, determines the event points statically, based solely on simple properties of the input data. In particular, each segment endpoint is an event point. We sort the segment endpoints by increasing x-coordinate and proceed from left to right. (If two or more endpoints are covertical, i.e., they have the same x-coordinate, we break the tie by putting all the covertical left endpoints before the covertical right endpoints. Within a set of covertical left endpoints, we put those with lower y-coordinates first, and do the same within a set of covertical right endpoints.) We insert a segment into the sweep-line status when its left endpoint is encountered, and we delete it from the sweep-line status when its right endpoint is encountered. Whenever two segments first become consecutive in the total order, we check whether they intersect.
The sweep-line status is a total order T, for which we require the following operations:
INSERT(T, s): insert segment s into T.
DELETE(T, s): delete segment s from T.
ABOVE(T, s): return the segment immediately above segment s in T.
BELOW(T, s): return the segment immediately below segment s in T.
If there are n segments in the input, we can perform each of the above operations in O(lg n) time using red-black trees. Recall that the red-black-tree operations in Chapter 13 involve comparing keys. We can replace the key comparisons by comparisons that use cross products to determine the relative ordering of two segments (see Exercise 33.2-2).
The following algorithm takes as input a set S of n line segments, returning the boolean value TRUE if any pair of segments in S intersects, and FALSE otherwise. The total order T is implemented by a red-black tree.
ANY-SEGMENTS-INTERSECT(S) 1 T ← Ø 2 sort the endpoints of the segments in S from left to right, breaking ties by putting left endpoints before right endpoints and breaking further ties by putting points with lower y-coordinates first 3 for each point p in the sorted list of endpoints 4 do if p is the left endpoint of a segment s 5 then INSERT(T, s) 6 if (ABOVE(T, s) exists and intersects s) or (BELOW(T, s) exists and intersects s) 7 then return TRUE 8 if p is the right endpoint of a segment s 9 then if both ABOVE(T, s) and BELOW(T, s) exist and ABOVE(T, s) intersects BELOW(T, s) 10 then return TRUE 11 DELETE(T, s) 12 return FALSE
Figure 33.5 illustrates the execution of the algorithm. Line 1 initializes the total order to be empty. Line 2 determines the event-point schedule by sorting the 2n segment endpoints from left to right, breaking ties as described above. Note that line 2 can be performed by lexicographically sorting the endpoints on (x, e, y), where x and y are the usual coordinates and e = 0 for a left endpoint and e = 1 for a right endpoint.
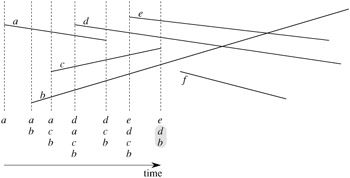
Each iteration of the for loop of lines 3-11 processes one event point p. If p is the left endpoint of a segment s, line 5 adds s to the total order, and lines 6-7 return TRUE if s intersects either of the segments it is consecutive with in the total order defined by the sweep line passing through p. (A boundary condition occurs if p lies on another segment s′. In this case, we require only that s and s′ be placed consecutively into T.) If p is the right endpoint of a segment s, then s is to be deleted from the total order. Lines 9-10 return TRUE if there is an intersection between the segments surrounding s in the total order defined by the sweep line passing through p; these segments will become consecutive in the total order when s is deleted. If these segments do not intersect, line 11 deletes segment s from the total order. Finally, if no intersections are found in processing all the 2n event points, line 12 returns FALSE.
To show that ANY-SEGMENTS-INTERSECT is correct, we will prove that the call ANY-SEGMENTS-INTERSECT(S) returns TRUE if and only if there is an intersection among the segments in S.
It is easy to see that ANY-SEGMENTS-INTERSECT returns TRUE (on lines 7 and 10) only if it finds an intersection between two of the input segments. Hence, if it returns TRUE, there is an intersection.
We also need to show the converse: that if there is an intersection, then ANY-SEGMENTS-INTERSECT returns TRUE. Let us suppose that there is at least one intersection. Let p be the leftmost intersection point, breaking ties by choosing the one with the lowest y-coordinate, and let a and b be the segments that intersect at p. Since no intersections occur to the left of p, the order given by T is correct at all points to the left of p. Because no three segments intersect at the same point, there exists a sweep line z at which a and b become consecutive in the total order.[2] Moreover, z is to the left of p or goes through p. There exists a segment endpoint q on sweep line z that is the event point at which a and b become consecutive in the total order. If p is on sweep line z, then q = p. If p is not on sweep line z, then q is to the left of p. In either case, the order given by T is correct just before q is encountered. (Here is where we use the lexicographic order in which the algorithm processes event points. Because p is the lowest of the leftmost intersection points, even if p is on sweep line z and there is another intersection point p′ on z, event point q = p is processed before the other intersection p′ can interfere with the total order T. Moreover, even if p is the left endpoint of one segment, say a, and the right endpoint of the other segment, say b, because left endpoint events occur before right endpoint events, segment b is in T when segment a is first encountered.) Either event point q is processed by ANY-SEGMENTS-INTERSECT or it is not processed.
If q is processed by ANY-SEGMENTS-INTERSECT, there are only two possibilities for the action taken:
Either a or b is inserted into T, and the other segment is above or below it in the total order. Lines 4-7 detect this case.
Segments a and b are already in T, and a segment between them in the total order is deleted, making a and b become consecutive. Lines 8-11 detect this case.
In either case, the intersection p is found and ANY-SEGMENTS-INTERSECT returns TRUE.
If event point q is not processed by ANY-SEGMENTS-INTERSECT, the procedure must have returned before processing all event points. This situation could have occurred only if ANY-SEGMENTS-INTERSECT had already found an intersection and returned TRUE.
Thus, if there is an intersection, ANY-SEGMENTS-INTERSECT returns TRUE. As we have already seen, if ANY-SEGMENTS-INTERSECT returns TRUE, there is an intersection. Therefore, ANY-SEGMENTS-INTERSECT always returns a correct answer.
If there are n segments in set S, then ANY-SEGMENTS-INTERSECT runs in time O(n lg n). Line 1 takes O(1) time. Line 2 takes O(n lg n) time, using merge sort or heapsort. Since there are 2n event points, the for loop of lines 3-11 iterates at most 2n times. Each iteration takes O(lg n) time, since each red-black-tree operation takes O(lg n) time and, using the method of Section 33.1, each intersection test takes O(1) time. The total time is thus O(n lg n).
Given two segments a and b that are comparable at x, show how to determine in O(1) time which of a >x b or b >x a holds. Assume that neither segment is vertical. (Hint: If a and b do not intersect, you can just use cross products. If a and b intersect-which you can of course determine using only cross products-you can still use only addition, subtraction, and multiplication, avoiding division. Of course, in the application of the >x relation used here, if a and b intersect, we can just stop and declare that we have found an intersection.)
Professor Maginot suggests that we modify ANY-SEGMENTS-INTERSECT so that instead of returning upon finding an intersection, it prints the segments that intersect and continues on to the next iteration of the for loop. The professor calls the resulting procedure PRINT-INTERSECTING-SEGMENTS and claims that it prints all intersections, from left to right, as they occur in the set of line segments. Show that the professor is wrong on two counts by giving a set of segments for which the first intersection found by PRINT-INTERSECTING-SEGMENTS is not the leftmost one and a set of segments for which PRINT-INTERSECTING-SEGMENTS fails to find all the intersections.
Give an O(n lg n)-time algorithm to determine whether an n-vertex polygon is simple.
Give an O(n lg n)-time algorithm to determine whether two simple polygons with a total of n vertices intersect.
A disk consists of a circle plus its interior and is represented by its center point and radius. Two disks intersect if they have any point in common. Give an O(n lg n)-time algorithm to determine whether any two disks in a set of n intersect.
Given a set of n line segments containing a total of k intersections, show how to output all k intersections in O((n + k) lg n) time.
Argue that ANY-SEGMENTS-INTERSECT works correctly even if three or more segments intersect at the same point.
Show that ANY-SEGMENTS-INTERSECT works correctly in the presence of vertical segments if the bottom endpoint of a vertical segment is processed as if it were a left endpoint and the top endpoint is processed as if it were a right endpoint. How does your answer to Exercise 33.2-2 change if vertical segments are allowed?
[2]If we allow three segments to intersect at the same point, there may be an intervening segment c that intersects both a and b at point p. That is, we may have a <w c and c <w b for all sweep lines w to the left of p for which a <w b. Exercise 33.2-8 asks you to show that ANY-SEGMENTS-INTERSECT is correct even if three segments do intersect at the same point.
| < Day Day Up > |