|
|
< Day Day Up > |
|
The NP-completeness of the circuit-satisfiability problem relies on a direct proof that L ≤P CIRCUIT-SAT for every language L ∈ NP. In this section, we shall show how to prove that languages are NP-complete without directly reducing every language in NP to the given language. We shall illustrate this methodology by proving that various formula-satisfiability problems are NP-complete. Section 34.5 provides many more examples of the methodology.
The following lemma is the basis of our method for showing that a language is NP-complete.
 |
If L is a language such that L′ ≤P L for some L′ ∈ NPC, then L is NP-hard. Moreover, if L ∈ NP, then L ∈ NPC.
Proof Since L′ is NP-complete, for all L′′∈ NP, we have L′′≤P L′. By supposition, L′ ≤P L, and thus by transitivity (Exercise 34.3-2), we have L′′ ≤P L, which shows that L is NP-hard. If L ∈ NP, we also have L ∈ NPC.
|
In other words, by reducing a known NP-complete language L′ to L, we implicitly reduce every language in NP to L. Thus, Lemma 34.8 gives us a method for proving that a language L is NP-complete:
Prove L ∈ NP.
Select a known NP-complete language L′.
Describe an algorithm that computes a function f mapping every instance x ∈ {0, 1}* of L′ to an instance f(x) of L.
Prove that the function f satisfies x ∈ L′ if and only if f (x) ∈ L for all x ∈ {0, 1}*.
Prove that the algorithm computing f runs in polynomial time.
(Steps 2-5 show that L is NP-hard.) This methodology of reducing from a single known NP-complete language is far simpler than the more complicated process of showing directly how to reduce from every language in NP. Proving CIRCUIT-SAT ∈ NPC has given us a "foot in the door." Knowing that the circuit-satisfiability problem is NP-complete now allows us to prove much more easily that other problems are NP-complete. Moreover, as we develop a catalog of known NP-complete problems, we will have more and more choices for languages from which to reduce.
We illustrate the reduction methodology by giving an NP-completeness proof for the problem of determining whether a boolean formula, not a circuit, is satisfiable. This problem has the historical honor of being the first problem ever shown to be NP-complete.
We formulate the (formula) satisfiability problem in terms of the language SAT as follows. An instance of SAT is a boolean formula φ composed of
n boolean variables: x1, x2, ..., xn;
m boolean connectives: any boolean function with one or two inputs and one output, such as ⊦ (AND), ⊥ (OR), ¬ (NOT), → (implication), ↔ (if and only if); and
parentheses. (Without loss of generality, we assume that there are no redundant parentheses, i.e., there is at most one pair of parentheses per boolean connective.)
It is easy to encode a boolean formula φ in a length that is polynomial in n + m. As in boolean combinational circuits, a truth assignment for a boolean formula φ is a set of values for the variables of φ, and a satisfying assignment is a truth assignment that causes it to evaluate to 1. A formula with a satisfying assignment is a satisfiable formula. The satisfiability problem asks whether a given boolean formula is satisfiable; in formal-language terms,
SAT = {〈φ〉 : φ is a satisfiable boolean formula}.
As an example, the formula
φ = ((x1 → x2) ⊥ ¬((¬x1 ↔ x3) ⊦ x4)) ⊦ ¬x2
has the satisfying assignment 〈x1 = 0, x2 = 0, x3 = 1, x4 = 1〉, since
and thus this formula φ belongs to SAT.
The naive algorithm to determine whether an arbitrary boolean formula is satisfiable does not run in polynomial time. There are 2n possible assignments in a formula φ with n variables. If the length of 〈φ〉 is polynomial in n, then checking every assignment requires Ω(2n) time, which is superpolynomial in the length of 〈φ〉. As the following theorem shows, a polynomial-time algorithm is unlikely to exist.
|
Satisfiability of boolean formulas is NP-complete.
Proof We start by arguing that SAT ∈ NP. Then we prove that CIRCUIT-SAT is NP-hard by showing that CIRCUIT-SAT ≤P SAT; by Lemma 34.8, this will prove the theorem.
To show that SAT belongs to NP, we show that a certificate consisting of a satisfying assignment for an input formula φ can be verified in polynomial time. The verifying algorithm simply replaces each variable in the formula with its corresponding value and then evaluates the expression, much as we did in equation (34.2) above. This task is easily done in polynomial time. If the expression evaluates to 1, the formula is satisfiable. Thus, the first condition of Lemma 34.8 for NP-completeness holds.
To prove that SAT is NP-hard, we show that CIRCUIT-SAT ≤P SAT. In other words, any instance of circuit satisfiability can be reduced in polynomial time to an instance of formula satisfiability. Induction can be used to express any boolean combinational circuit as a boolean formula. We simply look at the gate that produces the circuit output and inductively express each of the gate's inputs as formulas. The formula for the circuit is then obtained by writing an expression that applies the gate's function to its inputs' formulas.
Unfortunately, this straightforward method does not constitute a polynomial-time reduction. As Exercise 34.4-1 asks you to show, shared subformulas-which arise from gates whose output wires have fan-out of 2 or more-can cause the size of the generated formula to grow exponentially. Thus, the reduction algorithm must be somewhat more clever.
Figure 34.10 illustrates the basic idea of the reduction from CIRCUIT-SAT to SAT on the circuit from Figure 34.8(a). For each wire xi in the circuit C, the formula φ has a variable xi . The proper operation of a gate can now be expressed as a formula involving the variables of its incident wires. For example, the operation of the output AND gate is x10 ↔ (x7 ⊥ x8 ⊥ x9).
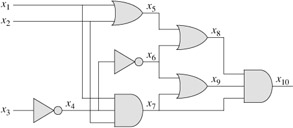
The formula φ produced by the reduction algorithm is the AND of the circuit-output variable with the conjunction of clauses describing the operation of each gate. For the circuit in the figure, the formula is
|
φ |
= |
x10 |
⊥ |
(x4 ↔ ¬x3) |
|
⊥ |
(x5 ↔ (x1 ⊦ x2)) |
|||
|
⊥ |
(x6 ↔ ¬x4) |
|||
|
⊥ |
(x7 ↔ (x1 ⊥ x2 ⊥ x4)) |
|||
|
⊥ |
(x8 ↔ (x5 ⊦ x6)) |
|||
|
⊥ |
(x9 ↔ (x6 ⊦ x7)) |
|||
|
⊥ |
(x10 (x7 ⊥ x8 ⊥ x9)). |
Given a circuit C, it is straightforward to produce such a formula φ in polynomial time.
Why is the circuit C satisfiable exactly when the formula φ is satisfiable? If C has a satisfying assignment, each wire of the circuit has a well-defined value, and the output of the circuit is 1. Therefore, the assignment of wire values to variables in φ makes each clause of φ evaluate to 1, and thus the conjunction of all evaluates to 1. Conversely, if there is an assignment that causes φ to evaluate to 1, the circuit C is satisfiable by an analogous argument. Thus, we have shown that CIRCUIT-SAT ≤P SAT, which completes the proof.
|
Many problems can be proved NP-complete by reduction from formula satisfiability. The reduction algorithm must handle any input formula, though, and this requirement can lead to a huge number of cases that must be considered. It is often desirable, therefore, to reduce from a restricted language of boolean formulas, so that fewer cases need be considered. Of course, we must not restrict the language so much that it becomes polynomial-time solvable. One convenient language is 3-CNF satisfiability, or 3-CNF-SAT.
We define 3-CNF satisfiability using the following terms. A literal in a boolean formula is an occurrence of a variable or its negation. A boolean formula is in conjunctive normal form, or CNF, if it is expressed as an AND of clauses, each of which is the OR of one or more literals. A boolean formula is in 3-conjunctive normal form, or 3-CNF, if each clause has exactly three distinct literals.
For example, the boolean formula
(x1 ⊦ ¬x1 ⊦ ¬x2) ⊥ (x3 ⊦ x2 ⊦ x4) ⊥ (¬x1 ⊦ ¬x3 ⊦ ¬x4)
is in 3-CNF. The first of its three clauses is (x1 ⊦ ¬x1 ⊦ ¬x2), which contains the three literals x1, ¬x1, and ¬x2.
In 3-CNF-SAT, we are asked whether a given boolean formula φ in 3-CNF is satisfiable. The following theorem shows that a polynomial-time algorithm that can determine the satisfiability of boolean formulas is unlikely to exist, even when they are expressed in this simple normal form.
|
Satisfiability of boolean formulas in 3-conjunctive normal form is NP-complete.
Proof The argument we used in the proof of Theorem 34.9 to show that SAT ∈ NP applies equally well here to show that 3-CNF-SAT ∈ NP. Thus, by Lemma 34.8, we need only show that SAT ≤P 3-CNF-SAT.
The reduction algorithm can be broken into three basic steps. Each step progressively transforms the input formula φ closer to the desired 3-conjunctive normal form.
The first step is similar to the one used to prove CIRCUIT-SAT ≤P SAT in Theorem 34.9. First, we construct a binary "parse" tree for the input formula φ, with literals as leaves and connectives as internal nodes. Figure 34.11 shows such a parse tree for the formula
| (34.3) |  |
Should the input formula contain a clause such as the OR of several literals, associativity can be used to parenthesize the expression fully so that every internal node in the resulting tree has 1 or 2 children. The binary parse tree can now be viewed as a circuit for computing the function.
Mimicking the reduction in the proof of Theorem 34.9, we introduce a variable yi for the output of each internal node. Then, we rewrite the original formula φ as the AND of the root variable and a conjunction of clauses describing the operation of each node. For the formula (34.3), the resulting expression is
|
φ' |
= |
y1 |
⊥ |
(y1 ↔ (y2 ⊥ ¬x2)) |
|
⊥ |
(y2 ↔ (y3 ⊦ y4)) |
|||
|
⊥ |
(y3 ↔ (x1 → x2)) |
|||
|
⊥ |
(y4 ↔ ¬y5) |
|||
|
⊥ |
(y5 ↔ (y6 ⊦ x4)) |
|||
|
⊥ |
(y6 ↔ (¬x1 → x3)) |
Observe that the formula φ' thus obtained is a conjunction of clauses 
, each of which has at most 3 literals. The only additional requirement is that each clause be an OR of literals.
The second step of the reduction converts each clause 
into conjunctive normal form. We construct a truth table for 
by evaluating all possible assignments to its variables. Each row of the truth table consists of a possible assignment of the variables of the clause, together with the value of the clause under that assignment. Using the truth-table entries that evaluate to 0, we build a formula in disjunctive normal form (or DNF)-an OR of AND's-that is equivalent to 
. We then convert this formula into a CNF formula 
by using DeMorgan's laws (equations (B.2)) to complement all literals and change OR's into AND's and AND's into OR's.
In our example, we convert the clause 
into CNF as follows. The truth table for 
is given in Figure 34.12. The DNF formula equivalent to 
is
(y1 ⊥ y2 ⊥ x2) ⊦ (y1 ⊥ ¬y2 ⊥ x2) ⊦ (y1 ⊥ ¬y2 ⊥ ¬x2) ⊦ (¬y1 ⊥ y2 ⊥ ¬x2).
|
|
y1 |
y2 |
x2 |
(y1 ↔ (y2 ⊥ ¬x2)) |
|---|---|---|---|
|
|
|||
|
1 |
1 |
1 |
0 |
|
1 |
1 |
0 |
1 |
|
1 |
0 |
1 |
0 |
|
1 |
0 |
0 |
0 |
|
0 |
1 |
1 |
1 |
|
0 |
1 |
0 |
0 |
|
0 |
0 |
1 |
1 |
|
0 |
0 |
0 |
1 |
|
Applying DeMorgan's laws, we get the CNF formula
which is equivalent to the original clause 
.
Each clause 
of the formula φ' has now been converted into a CNF formula 
, and thus φ' is equivalent to the CNF formula φ" consisting of the conjunction of the 
. Moreover, each clause of φ" has at most 3 literals.
The third and final step of the reduction further transforms the formula so that each clause has exactly 3 distinct literals. The final 3-CNF formula φ"' is constructed from the clauses of the CNF formula φ". It also uses two auxiliary variables that we shall call p and q. For each clause Ci of φ", we include the following clauses in φ"':
If Ci has 3 distinct literals, then simply include Ci as a clause of φ"'.
If Ci has 2 distinct literals, that is, if Ci = (l1 ⊦ l2), where l1 and l2 are literals, then include (l1 ⊦ l2 ⊦ p) ⊥ (l1 ⊦ l2 ⊦ ¬p) as clauses of φ"'. The literals p and ¬ p merely fulfill the syntactic requirement that there be exactly 3 distinct literals per clause: (l1 ⊦ l2 ⊦ p) ⊥ (l1 ⊦ l2 ⊦ ¬p) is equivalent to (l1 ⊦ l2) whether p = 0 or p = 1.
If Ci has just 1 distinct literal l, then include (l ⊦ p ⊦ q) ⊥ (l ⊦ p ⊦ ¬q) ⊥ (l ⊦ ¬p ⊦ q) ⊥ (l ⊦ ¬p ⊦ ¬q) as clauses of φ"'. Note that every setting of p and q causes the conjunction of these four clauses to evaluate to l.
We can see that the 3-CNF formula φ"' is satisfiable if and only if φ is satisfiable by inspecting each of the three steps. Like the reduction from CIRCUIT-SAT to SAT, the construction of φ' from φ in the first step preserves satisfiability. The second step produces a CNF formula φ" that is algebraically equivalent to φ'. The third step produces a 3-CNF formula φ"' that is effectively equivalent to φ", since any assignment to the variables p and q produces a formula that is algebraically equivalent to φ".
We must also show that the reduction can be computed in polynomial time. Constructing φ' from φ introduces at most 1 variable and 1 clause per connective in φ. Constructing φ" from φ' can introduce at most 8 clauses into φ" for each clause from φ', since each clause of φ' has at most 3 variables, and the truth table for each clause has at most 23 = 8 rows. The construction of φ"' from φ" introduces at most 4 clauses into φ"' for each clause of φ". Thus, the size of the resulting formula φ"' is polynomial in the length of the original formula. Each of the constructions can easily be accomplished in polynomial time.
|
|
Consider the straightforward (nonpolynomial-time) reduction in the proof of Theorem 34.9. Describe a circuit of size n that, when converted to a formula by this method, yields a formula whose size is exponential in n.
|
|
Professor Jagger proposes to show that SAT ≤P 3-CNF-SAT by using only the truth-table technique in the proof of Theorem 34.10, and not the other steps. That is, the professor proposes to take the boolean formula φ, form a truth table for its variables, derive from the truth table a formula in 3-DNF that is equivalent to ¬φ, and then negate and apply DeMorgan's laws to produce a 3-CNF formula equivalent to φ. Show that this strategy does not yield a polynomial-time reduction.
|
|
Show that the problem of determining whether a boolean formula is a tautology is complete for co-NP. (Hint: See Exercise 34.3-7.)
|
|
Show that the problem of determining the satisfiability of boolean formulas in disjunctive normal form is polynomial-time solvable.
|
|
Suppose that someone gives you a polynomial-time algorithm to decide formula satisfiability. Describe how to use this algorithm to find satisfying assignments in polynomial time.
|
|
Let 2-CNF-SAT be the set of satisfiable boolean formulas in CNF with exactly 2 literals per clause. Show that 2-CNF-SAT ∈ P. Make your algorithm as efficient as possible. (Hint: Observe that x ⊦ y is equivalent to ¬x → y. Reduce 2-CNF-SAT to a problem on a directed graph that is efficiently solvable.)
|
|
|
< Day Day Up > |
|
