|
|
< Day Day Up > |
|
Given a sequence a1, a2, ... of numbers, the finite sum a1 + a2 + ··· + an, where n is an nonnegative integer, can be written
If n = 0, the value of the summation is defined to be 0. The value of a finite series is always well defined, and its terms can be added in any order.
Given a sequence a1, a2, ... of numbers, the infinite sum a1 + a2 + ··· can be written
which is interpreted to mean
If the limit does not exist, the series diverges; otherwise, it converges. The terms of a convergent series cannot always be added in any order. We can, however, rearrange the terms of an absolutely convergent series, that is, a series 
for which the series 
also converges.
For any real number c and any finite sequences a1, a2, ..., an and b1, b2, ..., bn,
The linearity property is also obeyed by infinite convergent series.
The linearity property can be exploited to manipulate summations incorporating asymptotic notation. For example,
In this equation, the Θ-notation on the left-hand side applies to the variable k, but on the right-hand side, it applies to n. Such manipulations can also be applied to infinite convergent series.
For real x ≠ 1, the summation
is a geometric or exponential series and has the value
When the summation is infinite and |x| < 1, we have the infinite decreasing geometric series
For positive integers n, the nth harmonic number is
(We shall prove this bound in Section A.2.)
Additional formulas can be obtained by integrating or differentiating the formulas above. For example, by differentiating both sides of the infinite geometric series (A.6) and multiplying by x, we get
for |x| < 1.
For any sequence a0, a1, ..., an,
since each of the terms a1, a2, ..., an-1 is added in exactly once and subtracted out exactly once. We say that the sum telescopes. Similarly,
As an example of a telescoping sum, consider the series
Since we can rewrite each term as
we get
|
|
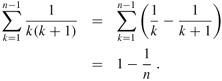
< Day Day Up > |
|
