|
|
< Day Day Up > |
|
This chapter reviews elementary combinatorics and probability theory. If you have a good background in these areas, you may want to skim the beginning of the chapter lightly and concentrate on the later sections. Most of the chapters do not require probability, but for some chapters it is essential.
Section C.1 reviews elementary results in counting theory, including standard formulas for counting permutations and combinations. The axioms of probability and basic facts concerning probability distributions are presented in Section C.2. Random variables are introduced in Section C.3, along with the properties of expectation and variance. Section C.4 investigates the geometric and binomial distributions that arise from studying Bernoulli trials. The study of the binomial distribution is continued in Section C.5, an advanced discussion of the "tails" of the distribution.
Counting theory tries to answer the question "How many?" without actually enumerating how many. For example, we might ask, "How many different n-bit numbers are there?" or "How many orderings of n distinct elements are there?" In this section, we review the elements of counting theory. Since some of the material assumes a basic understanding of sets, the reader is advised to start by reviewing the material in Section B.1.
A set of items that we wish to count can sometimes be expressed as a union of disjoint sets or as a Cartesian product of sets.
The rule of sum says that the number of ways to choose an element from one of two disjoint sets is the sum of the cardinalities of the sets. That is, if A and B are two finite sets with no members in common, then |A ∪ B| = |A| + |B|, which follows from equation (B.3). For example, each position on a car's license plate is a letter or a digit. The number of possibilities for each position is therefore 26 + 10 = 36, since there are 26 choices if it is a letter and 10 choices if it is a digit.
The rule of product says that the number of ways to choose an ordered pair is the number of ways to choose the first element times the number of ways to choose the second element. That is, if A and B are two finite sets, then |A × B| = |A| · |B|, which is simply equation (B.4). For example, if an ice-cream parlor offers 28 flavors of ice cream and 4 toppings, the number of possible sundaes with one scoop of ice cream and one topping is 28 · 4 = 112.
A string over a finite set S is a sequence of elements of S. For example, there are 8 binary strings of length 3:
000, 001, 010, 011, 100, 101, 110, 111.
We sometimes call a string of length k a k-string. A substring s' of a string s is an ordered sequence of consecutive elements of s. A k-substring of a string is a substring of length k. For example, 010 is a 3-substring of 01101001 (the 3-substring that begins in position 4), but 111 is not a substring of 01101001.
A k-string over a set S can be viewed as an element of the Cartesian product Sk of k-tuples; thus, there are |S|k strings of length k. For example, the number of binary k-strings is 2k. Intuitively, to construct a k-string over an n-set, we have n ways to pick the first element; for each of these choices, we have n ways to pick the second element; and so forth k times. This construction leads to the k-fold product n · n n = nk as the number of k-strings.
A permutation of a finite set S is an ordered sequence of all the elements of S, with each element appearing exactly once. For example, if S = {a, b, c}, there are 6 permutations of S:
abc, acb, bac, bca, cab, cba.
There are n! permutations of a set of n elements, since the first element of the sequence can be chosen in n ways, the second in n - 1 ways, the third in n - 2 ways, and so on.
A k-permutation of S is an ordered sequence of k elements of S, with no element appearing more than once in the sequence. (Thus, an ordinary permutation is just an n-permutation of an n-set.) The twelve 2-permutations of the set {a, b, c, d} are
ab, ac, ad, ba, bc, bd, ca, cb, cd, da, db, dc.
The number of k-permutations of an n-set is
since there are n ways of choosing the first element, n - 1 ways of choosing the second element, and so on until k elements are selected, the last being a selection from n - k + 1 elements.
A k-combination of an n-set S is simply a k-subset of S. For example, there are six 2-combinations of the 4-set {a, b, c, d}:
ab, ac, ad, bc, bd, cd.
(Here we use the shorthand of denoting the 2-set {a, b} by ab, and so on.) We can construct a k-combination of an n-set by choosing k distinct (different) elements from the n-set.
The number of k-combinations of an n-set can be expressed in terms of the number of k-permutations of an n-set. For every k-combination, there are exactly k! permutations of its elements, each of which is a distinct k-permutation of the n-set. Thus, the number of k-combinations of an n-set is the number of k-permutations divided by k!; from equation (C.1), this quantity is
For k = 0, this formula tells us that the number of ways to choose 0 elements from an n-set is 1 (not 0), since 0! = 1.
We use the notation 
(read "n choose k") to denote the number of k-combinations of an n-set. From equation (C.2), we have
This formula is symmetric in k and n - k:
These numbers are also known as binomial coefficients, due to their appearance in the binomial expansion:
A special case of the binomial expansion occurs when x = y = 1:
This formula corresponds to counting the 2n binary n-strings by the number of 1's they contain: there are 
binary n-strings containing exactly k 1's, since there are 
ways to choose k out of the n positions in which to place the 1's.
There are many identities involving binomial coefficients. The exercises at the kend of this section give you the opportunity to prove a few.
We sometimes need to bound the size of a binomial coefficient. For 1 ≤ k ≤ n, we have the lower bound
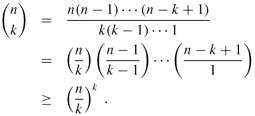
Taking advantage of the inequality k! ≥ (k/e)k derived from Stirling's approximation (3.17), we obtain the upper bounds
| (C.5) |  |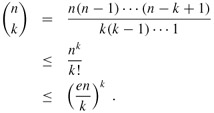
For all 0 ≤ k ≤ n, we can use induction (see Exercise C.1-12) to prove the bound
where for convenience we assume that 00 = 1. For k = λn, where 0 ≤ λ ≤ 1, this bound can be rewritten as
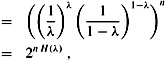
where
is the (binary) entropy function and where, for convenience, we assume that 0 lg 0 = 0, so that H(0) = H(1) = 0.
 |
How many k-substrings does an n-string have? (Consider identical k-substrings at different positions as different.) How many substrings does an n-string have in total?
|
|
An n-input, m-output boolean function is a function from {TRUE, FALSE}n to {TRUE, FALSE}m. How many n-input, 1-output boolean functions are there? How many n-input, m-output boolean functions are there?
|
|
In how many ways can n professors sit around a circular conference table? Consider two seatings to be the same if one can be rotated to form the other.
|
|
How many ways are there to choose from the set {1, 2,..., 100} three distinct numbers so that their sum is even?
|
|
To choose k objects from n, you can make one of the objects distinguished and consider whether the distinguished object is chosen. Use this approach to prove that
|
|
Using the result of Exercise C.1-7, make a table for n = 0, 1,..., 6 and 0 ≤ k ≤ n of the binomial coefficients 
with 
at the top, 
and 
on the next line, and so forth. Such a table of binomial coefficients is called Pascal's triangle.
|
|
Show that for any n ≥ 0 and 0 ≤ k = n, the maximum value of 
is achieved k when k = ⌊n/2⌋ or k = ⌉n/2⌈.
|
|
Argue that for any n ≥ 0, j ≥ 0, k ≥ 0, and j + k ≤ n,
| (C.9) |  |
Provide both an algebraic proof and an argument based on a method for choosing j + k items out of n. Give an example in which equality does not hold.
|
|
By differentiating the entropy function H(λ), show that it achieves its maximum value at λ = 1/2. What is H(1/2)?
|
|
|
< Day Day Up > |
|
