4.2 The recursion-tree method

Although the substitution method can provide a succinct proof that a solution to a recurrence is correct, it is sometimes difficult to come up with a good guess. Drawing out a recursion tree, as we did in our analysis of the merge sort recurrence in Section 2.3.2, is a straightforward way to devise a good guess. In a recursion tree, each node represents the cost of a single subproblem somewhere in the set of recursive function invocations. We sum the costs within each level of the tree to obtain a set of per-level costs, and then we sum all the per-level costs to determine the total cost of all levels of the recursion. Recursion trees are particularly useful when the recurrence describes the running time of a divide-and-conquer algorithm.

A recursion tree is best used to generate a good guess, which is then verified by the substitution method. When using a recursion tree to generate a good guess, you can often tolerate a small amount of "sloppiness," since you will be verifying your guess later on. If you are very careful when drawing out a recursion tree and summing the costs, however, you can use a recursion tree as a direct proof of a solution to a recurrence. In this section, we will use recursion trees to generate good guesses, and in Section 4.4, we will use recursion trees directly to prove the theorem that forms the basis of the master method.

For example, let us see how a recursion tree would provide a good guess for the recurrence T (n) = 3T (⌊n/4⌋) + Θ(n²). We start by focusing on finding an upper bound for the solution. Because we know that floors and ceilings are usually insubstantial in solving recurrences (here's an example of sloppiness that we can tolerate), we create a recursion tree for the recurrence T (n) = 3T(n/4) + cn², having written out the implied constant coefficient c > 0.

Figure 4.1 shows the derivation of the recursion tree for T (n) = 3T (n/4) + cn². For convenience, we assume that n is an exact power of 4 (another example of tolerable sloppiness). Part (a) of the figure shows T (n), which is expanded in part (b) into an equivalent tree representing the recurrence. The cn² term at the root represents the cost at the top level of recursion, and the three subtrees of the root represent the costs incurred by the subproblems of size n/4. Part (c) shows this process carried one step further by expanding each node with cost T (n/4) from part (b). The cost for each of the three children of the root is c(n/4)². We continue expanding each node in the tree by breaking it into its constituent parts as determined by the recurrence.

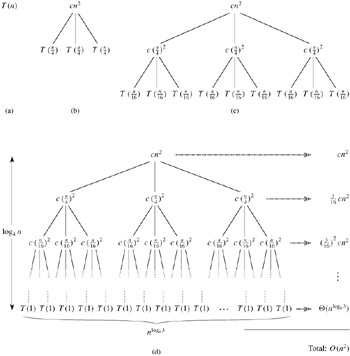
Because subproblem sizes decrease as we get further from the root, we eventually must reach a boundary condition. How far from the root do we reach one? The subproblem size for a node at depth i is n/4ⁱ. Thus, the subproblem size hits n = 1 when n/4ⁱ = 1 or, equivalently, when i = log₄ n. Thus, the tree has log ₄n + 1 levels (0, 1, 2,..., log₄ n).

Next we determine the cost at each level of the tree. Each level has three times more nodes than the level above, and so the number of nodes at depth i is 3ⁱ. Because subproblem sizes reduce by a factor of 4 for each level we go down from the root, each node at depth i, for i = 0, 1, 2,..., log₄ n - 1, has a cost of c(n/4ⁱ)². Multiplying, we see that the total cost over all nodes at depth i, for i = 0, 1, 2,..., log₄ n - 1, is 3ⁱ c(n/4ⁱ)² = (3/16)ⁱ cn². The last level, at depth log₄ n, has nodes, each contributing cost T (1), for a total cost of , which is .

Now we add up the costs over all levels to determine the cost for the entire tree:

This last formula looks somewhat messy until we realize that we can again take advantage of small amounts of sloppiness and use an infinite decreasing geometric series as an upper bound. Backing up one step and applying equation (A.6), we have

Thus, we have derived a guess of T (n) = O(n²) for our original recurrence T (n) = 3T (⌊n/4⌋) + Θ(n²). In this example, the coefficients of cn² form a decreasing geometric series and, by equation (A.6), the sum of these coefficients is bounded from above by the constant 16/13. Since the root's contribution to the total cost is cn², the root contributes a constant fraction of the total cost. In other words, the total cost of the tree is dominated by the cost of the root.

In fact, if O(n²) is indeed an upper bound for the recurrence (as we shall verify in a moment), then it must be a tight bound. Why? The first recursive call contributes a cost of Θ(n²), and so Ω (n²) must be a lower bound for the recurrence.

Now we can use the substitution method to verify that our guess was correct, that is, T (n) = O(n²) is an upper bound for the recurrence T (n) = 3T (⌊n/4⌋)+Θ(n²). We want to show that T (n) ≤ dn² for some constant d > 0. Using the same constant c > 0 as before, we have

where the last step holds as long as d ≥ (16/13)c.

As another, more intricate example, Figure 4.2 shows the recursion tree for T (n) = T(n/3) + T(2n/3) + O(n).

(Again, we omit floor and ceiling functions for simplicity.) As before, we let c represent the constant factor in the O(n) term. When we add the values across the levels of the recursion tree, we get a value of cn for every level. The longest path from the root to a leaf is n → (2/3)n → (2/3)²n → ··· → 1. Since (2/3)^kn = 1 when k = log_3/2 n, the height of the tree is log_3/2 n.

Intuitively, we expect the solution to the recurrence to be at most the number of levels times the cost of each level, or O(cn log_3/2 n) = O(n lg n). The total cost is evenly distributed throughout the levels of the recursion tree. There is a complication here: we have yet to consider the cost of the leaves. If this recursion tree were a complete binary tree of height log_3/2 n, there would be leaves. Since the cost of each leaf is a constant, the total cost of all leaves would then be , which is ω(n lg n). This recursion tree is not a complete binary tree, however, and so it has fewer than leaves. Moreover, as we go down from the root, more and more internal nodes are absent. Consequently, not all levels contribute a cost of exactly cn; levels toward the bottom contribute less. We could work out an accurate accounting of all costs, but remember that we are just trying to come up with a guess to use in the substitution method. Let us tolerate the sloppiness and attempt to show that a guess of O(n lg n) for the upper bound is correct.

Indeed, we can use the substitution method to verify that O(n lg n) is an upper bound for the solution to the recurrence. We show that T (n) ≤ dn lg n, where d is a suitable positive constant. We have

as long as d ≥ c/(lg 3 - (2/3)). Thus, we did not have to perform a more accurate accounting of costs in the recursion tree.