6.2 Maintaining the heap property

MAX-HEAPIFY is an important subroutine for manipulating max-heaps. Its inputs are an array A and an index i into the array. When MAX-HEAPIFY is called, it is assumed that the binary trees rooted at LEFT(i) and RIGHT(i) are max-heaps, but that A[i] may be smaller than its children, thus violating the max-heap property. The function of MAX-HEAPIFY is to let the value at A[i] "float down" in the max-heap so that the subtree rooted at index i becomes a max-heap.

MAX-HEAPIFY(A, i)
 1 l ← LEFT(i)
 2 r ← RIGHT(i)
 3 if l ≤ heap-size[A] and A[l] > A[i]
 4    then largest ← l
 5    else largest ← i
 6 if r ≤ heap-size[A] and A[r] > A[largest]
 7    then largest ← r
 8 if largest ≠ i
 9    then exchange A[i] ↔ A[largest]
10         MAX-HEAPIFY(A, largest)

Figure 6.2 illustrates the action of MAX-HEAPIFY. At each step, the largest of the elements A[i], A[LEFT(i)], and A[RIGHT(i)] is determined, and its index is stored in largest. If A[i] is largest, then the subtree rooted at node i is a max-heap and the procedure terminates. Otherwise, one of the two children has the largest element, and A[i] is swapped with A[largest], which causes node i and its children to satisfy the max-heap property. The node indexed by largest, however, now has the original value A[i], and thus the subtree rooted at largest may violate the max-heap property. Consequently, MAX-HEAPIFY must be called recursively on that subtree.

Figure 6.2: The action of MAX-HEAPIFY(A, 2), where heap-size[A] = 10. (a) The initial configuration, with A[2] at node i = 2 violating the max-heap property since it is not larger than both children. The max-heap property is restored for node 2 in (b) by exchanging A[2] with A[4], which destroys the max-heap property for node 4. The recursive call MAX-HEAPIFY(A, 4) now has i = 4. After swapping A[4] with A[9], as shown in (c), node 4 is fixed up, and the recursive call MAX-HEAPIFY(A, 9) yields no further change to the data structure.

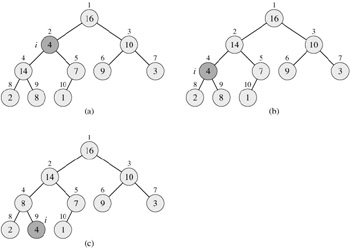
The running time of MAX-HEAPIFY on a subtree of size n rooted at given node i is the Θ(1) time to fix up the relationships among the elements A[i], A[LEFT(i)], and A[RIGHT(i)], plus the time to run MAX-HEAPIFY on a subtree rooted at one of the children of node i. The children's subtrees each have size at most 2n/3-the worst case occurs when the last row of the tree is exactly half full-and the running time of MAX-HEAPIFY can therefore be described by the recurrence

T (n) ≤ T(2n/3) + Θ(1).

The solution to this recurrence, by case 2 of the master theorem (Theorem 4.1), is T (n) = O(lg n). Alternatively, we can characterize the running time of MAX-HEAPIFY on a node of height h as O(h).

Exercises 6.2-1

Using Figure 6.2 as a model, illustrate the operation of MAX-HEAPIFY(A, 3) on the array A = 〈27, 17, 3, 16, 13, 10, 1, 5, 7, 12, 4, 8, 9, 0〉.

Exercises 6.2-2

Starting with the procedure MAX-HEAPIFY, write pseudocode for the procedure MIN-HEAPIFY(A, i), which performs the corresponding manipulation on a min-heap. How does the running time of MIN-HEAPIFY compare to that of MAX-HEAPIFY?

Exercises 6.2-3

What is the effect of calling MAX-HEAPIFY(A, i) when the element A[i] is larger than its children?

Exercises 6.2-4

What is the effect of calling MAX-HEAPIFY(A, i) for i > heap-size[A]/2?

Exercises 6.2-5

The code for MAX-HEAPIFY is quite efficient in terms of constant factors, except possibly for the recursive call in line 10, which might cause some compilers to produce inefficient code. Write an efficient MAX-HEAPIFY that uses an iterative control construct (a loop) instead of recursion.

Exercises 6.2-6

Show that the worst-case running time of MAX-HEAPIFY on a heap of size n is Ω(lg n). (Hint: For a heap with n nodes, give node values that cause MAX-HEAPIFY to be called recursively at every node on a path from the root down to a leaf.)