| < Day Day Up > |
We can use the procedure MAX-HEAPIFY in a bottom-up manner to convert an array A[1 ‥ n], where n = length[A], into a max-heap. By Exercise 6.1-7, the elements in the subarray A[(⌊n/2⌋+1) ‥ n] are all leaves of the tree, and so each is a 1-element heap to begin with. The procedure BUILD-MAX-HEAP goes through the remaining nodes of the tree and runs MAX-HEAPIFY on each one.
BUILD-MAX-HEAP(A) 1 heap-size[A] ← length[A] 2 for i ← ⌊length[A]/2⌋ downto 1 3 do MAX-HEAPIFY(A, i)
Figure 6.3 shows an example of the action of BUILD-MAX-HEAP.
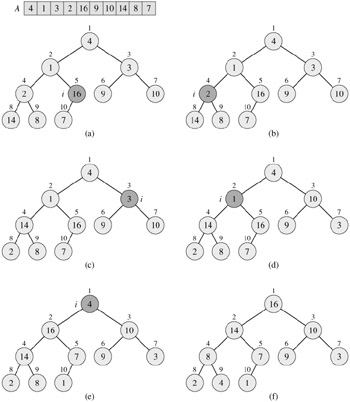
To show why BUILD-MAX-HEAP works correctly, we use the following loop invariant:
At the start of each iteration of the for loop of lines 2-3, each node i + 1, i + 2, . . . , n is the root of a max-heap.
We need to show that this invariant is true prior to the first loop iteration, that each iteration of the loop maintains the invariant, and that the invariant provides a useful property to show correctness when the loop terminates.
Initialization: Prior to the first iteration of the loop, i = ⌊n/2⌋. Each node ⌊n/2⌋ + 1, ⌊n/2⌋ + 2, . . . , n is a leaf and is thus the root of a trivial max-heap.
Maintenance: To see that each iteration maintains the loop invariant, observe that the children of node i are numbered higher than i. By the loop invariant, therefore, they are both roots of max-heaps. This is precisely the condition required for the call MAX-HEAPIFY(A, i) to make node i a max-heap root. Moreover, the MAX-HEAPIFY call preserves the property that nodes i + 1, i + 2, . . . , n are all roots of max-heaps. Decrementing i in the for loop update reestablishes the loop invariant for the next iteration.
Termination: At termination, i = 0. By the loop invariant, each node 1, 2, . . . , n is the root of a max-heap. In particular, node 1 is.
We can compute a simple upper bound on the running time of BUILD-MAX-HEAP as follows. Each call to MAX-HEAPIFY costs O(lg n) time, and there are O(n) such calls. Thus, the running time is O(n lg n). This upper bound, though correct, is not asymptotically tight.
We can derive a tighter bound by observing that the time for MAX-HEAPIFY to run at a node varies with the height of the node in the tree, and the heights of most nodes are small. Our tighter analysis relies on the properties that an n-element heap has height ⌊lg n⌋ (see Exercise 6.1-2) and at most ⌈n/2h+1⌉ nodes of any height h (see Exercise 6.3-3).
The time required by MAX-HEAPIFY when called on a node of height h is O(h), so we can express the total cost of BUILD-MAX-HEAP as
The last summation can be evaluated by substituting x = 1/2 in the formula (A.8), which yields
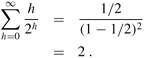
Thus, the running time of BUILD-MAX-HEAP can be bounded as
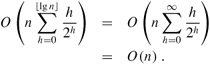
Hence, we can build a max-heap from an unordered array in linear time.
We can build a min-heap by the procedure BUILD-MIN-HEAP, which is the same as BUILD-MAX-HEAP but with the call to MAX-HEAPIFY in line 3 replaced by a call to MIN-HEAPIFY (see Exercise 6.2-2). BUILD-MIN-HEAP produces a min-heap from an unordered linear array in linear time.
Using Figure 6.3 as a model, illustrate the operation of BUILD-MAX-HEAP on the array A = 〈5, 3, 17, 10, 84, 19, 6, 22, 9〉.
| < Day Day Up > |