6.4 The heapsort algorithm

The heapsort algorithm starts by using BUILD-MAX-HEAP to build a max-heap on the input array A[1 ‥ n], where n = length[A]. Since the maximum element of the array is stored at the root A[1], it can be put into its correct final position by exchanging it with A[n]. If we now "discard" node n from the heap (by decrementing heap-size[A]), we observe that A[1 ‥ (n - 1)] can easily be made into a max-heap. The children of the root remain max-heaps, but the new root element may violate the max-heap property. All that is needed to restore the max-heap property, however, is one call to MAX-HEAPIFY(A, 1), which leaves a max-heap in A[1 ‥ (n - 1)]. The heapsort algorithm then repeats this process for the max-heap of size n - 1 down to a heap of size 2. (See Exercise 6.4-2 for a precise loop invariant.)

HEAPSORT(A)
1 BUILD-MAX-HEAP(A)
2 for i ← length[A] downto 2
3    do exchange A[1] ↔ A[i]
4       heap-size[A] ← heap-size[A] - 1
5       MAX-HEAPIFY(A, 1)

Figure 6.4 shows an example of the operation of heapsort after the max-heap is initially built. Each max-heap is shown at the beginning of an iteration of the for loop of lines 2-5.

Figure 6.4: The operation of HEAPSORT. (a) The max-heap data structure just after it has been built by BUILD-MAX-HEAP. (b)-(j) The max-heap just after each call of MAX-HEAPIFY in line 5. The value of i at that time is shown. Only lightly shaded nodes remain in the heap. (k) The resulting sorted array A.

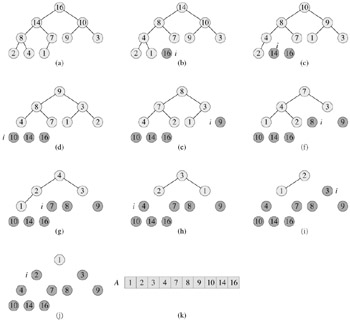
The HEAPSORT procedure takes time O(n lg n), since the call to BUILD-MAX-HEAP takes time O(n) and each of the n - 1 calls to MAX-HEAPIFY takes time O(lg n).

Exercises 6.4-1

Using Figure 6.4 as a model, illustrate the operation of HEAPSORT on the array A = 〈5, 13, 2, 25, 7, 17, 20, 8, 4〉.

Exercises 6.4-2

Argue the correctness of HEAPSORT using the following loop invariant:

At the start of each iteration of the for loop of lines 2-5, the subarray A[1 ‥ i] is a max-heap containing the i smallest elements of A[1 ‥ n], and the subarray A[i + 1 ‥ n] contains the n - i largest elements of A[1 ‥ n], sorted.

Exercises 6.4-3

What is the running time of heapsort on an array A of length n that is already sorted in increasing order? What about decreasing order?

Exercises 6.4-4

Show that the worst-case running time of heapsort is Ω(n lg n).

Exercises 6.4-5: ★

Show that when all elements are distinct, the best-case running time of heapsort is Ω(n lg n).