12.1 What is a binary search tree?

A binary search tree is organized, as the name suggests, in a binary tree, as shown in Figure 12.1. Such a tree can be represented by a linked data structure in which each node is an object. In addition to a key field and satellite data, each node contains fields left, right, and p that point to the nodes corresponding to its left child, its right child, and its parent, respectively. If a child or the parent is missing, the appropriate field contains the value NIL. The root node is the only node in the tree whose parent field is NIL.

Figure 12.1: Binary search trees. For any node x, the keys in the left subtree of x are at most key[x], and the keys in the right subtree of x are at least key[x]. Different binary search trees can represent the same set of values. The worst-case running time for most search-tree operations is proportional to the height of the tree. (a) A binary search tree on 6 nodes with height 2. (b) A less efficient binary search tree with height 4 that contains the same keys.

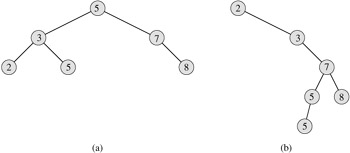
The keys in a binary search tree are always stored in such a way as to satisfy the binary-search-tree property:

Let x be a node in a binary search tree. If y is a node in the left subtree of x, then key[y] ≤ key[x]. If y is a node in the right subtree of x, then key[x] ≤ key[y].

Thus, in Figure 12.1(a), the key of the root is 5, the keys 2, 3, and 5 in its left subtree are no larger than 5, and the keys 7 and 8 in its right subtree are no smaller than 5. The same property holds for every node in the tree. For example, the key 3 in Figure 12.1(a) is no smaller than the key 2 in its left subtree and no larger than the key 5 in its right subtree.

The binary-search-tree property allows us to print out all the keys in a binary search tree in sorted order by a simple recursive algorithm, called an inorder tree walk. This algorithm is so named because the key of the root of a subtree is printed between the values in its left subtree and those in its right subtree. (Similarly, a preorder tree walk prints the root before the values in either subtree, and a postorder tree walk prints the root after the values in its subtrees.) To use the following procedure to print all the elements in a binary search tree T , we call INORDER-TREE-WALK (root[T]).

INORDER-TREE-WALK(x)
1  if x ≠ NIL
2     then INORDER-TREE-WALK(left[x])
3          print key[x]
4          INORDER-TREE-WALK(right[x])

As an example, the inorder tree walk prints the keys in each of the two binary search trees from Figure 12.1 in the order 2, 3, 5, 5, 7, 8. The correctness of the algorithm follows by induction directly from the binary-search-tree property.

It takes Θ(n) time to walk an n-node binary search tree, since after the initial call, the procedure is called recursively exactly twice for each node in the tree-once for its left child and once for its right child. The following theorem gives a more formal proof that it takes linear time to perform an inorder tree walk.

Theorem 12.1

If x is the root of an n-node subtree, then the call INORDER-TREE-WALK(x) takes Θ(n) time.

Proof Let T(n) denote the time taken by INORDER-TREE-WALK when it is called on the root of an n-node subtree. INORDER-TREE-WALK takes a small, constant amount of time on an empty subtree (for the test x ≠ NIL), and so T(0) = c for some positive constant c.

For n > 0, suppose that INORDER-TREE-WALK is called on a node x whose left subtree has k nodes and whose right subtree has n - k - 1 nodes. The time to perform INORDER-TREE-WALK(x) is T(n) = T(k) + T(n - k - 1) + d for some positive constant d that reflects the time to execute INORDER-TREE-WALK(x), exclusive of the time spent in recursive calls.

We use the substitution method to show that T(n) = Θ(n) by proving that T(n) = (c + d)n + c. For n = 0, we have (c + d) · 0 + c = c = T(0). For n > 0, we have

T(n)	=	T(k) + T(n - k - 1) + d
	=	((c + d)k + c) + ((c + d)(n - k - 1) + c) + d
	=	(c + d)n + c - (c + d) + c + d
	=	(c + d)n + c,

which completes the proof.

Exercises 12.1-1

For the set of keys {1, 4, 5, 10, 16, 17, 21}, draw binary search trees of height 2, 3, 4, 5, and 6.

Exercises 12.1-2

What is the difference between the binary-search-tree property and the min-heap property (see page 129)? Can the min-heap property be used to print out the keys of an n-node tree in sorted order in O(n) time? Explain how or why not.

Exercises 12.1-3

Give a nonrecursive algorithm that performs an inorder tree walk. (Hint: There is an easy solution that uses a stack as an auxiliary data structure and a more complicated but elegant solution that uses no stack but assumes that two pointers can be tested for equality.)

Exercises 12.1-4

Give recursive algorithms that perform preorder and postorder tree walks in Θ(n) time on a tree of n nodes.

Exercises 12.1-5

Argue that since sorting n elements takes Ω(n lg n) time in the worst case in the comparison model, any comparison-based algorithm for constructing a binary search tree from an arbitrary list of n elements takes Ω(n lg n) time in the worst case.