| < Day Day Up > |
A common operation performed on a binary search tree is searching for a key stored in the tree. Besides the SEARCH operation, binary search trees can support such queries as MINIMUM, MAXIMUM, SUCCESSOR, and PREDECESSOR. In this section, we shall examine these operations and show that each can be supported in time O(h) on a binary search tree of height h.
We use the following procedure to search for a node with a given key in a binary search tree. Given a pointer to the root of the tree and a key k, TREE-SEARCH returns a pointer to a node with key k if one exists; otherwise, it returns NIL.
TREE-SEARCH (x, k)
1 if x= NIL or k = key[x]
2 then return x
3 if k < key[x]
4 then return TREE-SEARCH(left[x], k)
5 else return TREE-SEARCH(right[x], k)
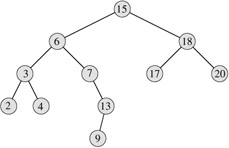
The procedure begins its search at the root and traces a path downward in the tree, as shown in Figure 12.2. For each node x it encounters, it compares the key k with key[x]. If the two keys are equal, the search terminates. If k is smaller than key[x], the search continues in the left subtree of x, since the binary-search-tree property implies that k could not be stored in the right subtree. Symmetrically, if k is larger than key[x], the search continues in the right subtree. The nodes encountered during the recursion form a path downward from the root of the tree, and thus the running time of TREE-SEARCH is O(h), where h is the height of the tree.
The same procedure can be written iteratively by "unrolling" the recursion into a while loop. On most computers, this version is more efficient.
ITERATIVE-TREE-SEARCH(x, k) 1 while x ≠ NIL and k ≠ key[x] 2 do if k < key[x] 3 then x ← left[x] 4 else x ← right[x] 5 return x
An element in a binary search tree whose key is a minimum can always be found by following left child pointers from the root until a NIL is encountered, as shown in Figure 12.2. The following procedure returns a pointer to the minimum element in the subtree rooted at a given node x.
TREE-MINIMUM (x) 1 while left[x] ≠ NIL 2 do x ← left[x] 3 return x
The binary-search-tree property guarantees that TREE-MINIMUM is correct. If a node x has no left subtree, then since every key in the right subtree of x is at least as large as key[x], the minimum key in the subtree rooted at x is key[x]. If node x has a left subtree, then since no key in the right subtree is smaller than key[x] and every key in the left subtree is not larger than key[x], the minimum key in the subtree rooted at x can be found in the subtree rooted at left[x].
The pseudocode for TREE-MAXIMUM is symmetric.
TREE-MAXIMUM(x) 1 while right[x] ≠ NIL 2 do x ← right[x] 3 return x
Both of these procedures run in O(h) time on a tree of height h since, as in TREE-SEARCH, the sequence of nodes encountered forms a path downward from the root.
Given a node in a binary search tree, it is sometimes important to be able to find its successor in the sorted order determined by an inorder tree walk. If all keys are distinct, the successor of a node x is the node with the smallest key greater than key[x]. The structure of a binary search tree allows us to determine the successor of a node without ever comparing keys. The following procedure returns the successor of a node x in a binary search tree if it exists, and NIL if x has the largest key in the tree.
TREE-SUCCESSOR(x) 1 if right[x] ≠ NIL 2 then return TREE-MINIMUM (right[x]) 3 y ← p[x] 4 while y ≠ NIL and x = right[y] 5 do x ← y 6 y ← p[y] 7 return y
The code for TREE-SUCCESSOR is broken into two cases. If the right subtree of node x is nonempty, then the successor of x is just the leftmost node in the right subtree, which is found in line 2 by calling TREE-MINIMUM(right[x]). For example, the successor of the node with key 15 in Figure 12.2 is the node with key 17.
On the other hand, as Exercise 12.2-6 asks you to show, if the right subtree of node x is empty and x has a successor y, then y is the lowest ancestor of x whose left child is also an ancestor of x. In Figure 12.2, the successor of the node with key 13 is the node with key 15. To find y, we simply go up the tree from x until we encounter a node that is the left child of its parent; this is accomplished by lines 3-7 of TREE-SUCCESSOR.
The running time of TREE-SUCCESSOR on a tree of height h is O(h), since we either follow a path up the tree or follow a path down the tree. The procedure TREE-PREDECESSOR, which is symmetric to TREE-SUCCESSOR, also runs in time O(h).
Even if keys are not distinct, we define the successor and predecessor of any node x as the node returned by calls made to TREE-SUCCESSOR(x) and TREE-PREDECESSOR(x), respectively.
In summary, we have proved the following theorem.
The dynamic-set operations SEARCH, MINIMUM, MAXIMUM, SUCCESSOR, and PREDECESSOR can be made to run in O(h) time on a binary search tree of height h.
Suppose that we have numbers between 1 and 1000 in a binary search tree and want to search for the number 363. Which of the following sequences could not be the sequence of nodes examined?
2, 252, 401, 398, 330, 344, 397, 363.
924, 220, 911, 244, 898, 258, 362, 363.
925, 202, 911, 240, 912, 245, 363.
2, 399, 387, 219, 266, 382, 381, 278, 363.
935, 278, 347, 621, 299, 392, 358, 363.
Professor Bunyan thinks he has discovered a remarkable property of binary search trees. Suppose that the search for key k in a binary search tree ends up in a leaf. Consider three sets: A, the keys to the left of the search path; B, the keys on the search path; and C, the keys to the right of the search path. Professor Bunyan claims that any three keys a ∈ A, b ∈ B, and c ∈ C must satisfy a ≤ b ≤ c. Give a smallest possible counterexample to the professor's claim.
Show that if a node in a binary search tree has two children, then its successor has no left child and its predecessor has no right child.
Consider a binary search tree T whose keys are distinct. Show that if the right subtree of a node x in T is empty and x has a successor y, then y is the lowest ancestor of x whose left child is also an ancestor of x. (Recall that every node is its own ancestor.)
An inorder tree walk of an n-node binary search tree can be implemented by finding the minimum element in the tree with TREE-MINIMUM and then making n-1 calls to TREE-SUCCESSOR. Prove that this algorithm runs in Θ(n) time.
| < Day Day Up > |