| < Day Day Up > |
The operations of insertion and deletion cause the dynamic set represented by a binary search tree to change. The data structure must be modified to reflect this change, but in such a way that the binary-search-tree property continues to hold. As we shall see, modifying the tree to insert a new element is relatively straight-forward, but handling deletion is somewhat more intricate.
To insert a new value v into a binary search tree T , we use the procedure TREE-INSERT. The procedure is passed a node z for which key[z] = v, left[z] = NIL, and right[z] = NIL. It modifies T and some of the fields of z in such a way that z is inserted into an appropriate position in the tree.
TREE-INSERT(T, z) 1 y ← NIL 2 x ← root[T] 3 while x ≠ NIL 4 do y ← x 5 if key[z] < key[x] 6 then x ← left[x] 7 else x ← right[x] 8 p[z] ← y 9 if y = NIL 10 then root[T] ← z ⊹ Tree T was empty 11 else if key[z] < key[y] 12 then left[y] ← z 13 else right[y] ← z
Figure 12.3 shows how TREE-INSERT works. Just like the procedures TREE-SEARCH and ITERATIVE-TREE-SEARCH, TREE-INSERT begins at the root of the tree and traces a path downward. The pointer x traces the path, and the pointer y is maintained as the parent of x. After initialization, the while loop in lines 3-7 causes these two pointers to move down the tree, going left or right depending on the comparison of key[z] with key[x], until x is set to NIL. This NIL occupies the position where we wish to place the input item z. Lines 8-13 set the pointers that cause z to be inserted.
Like the other primitive operations on search trees, the procedure TREE-INSERT runs in O(h) time on a tree of height h.
The procedure for deleting a given node z from a binary search tree takes as an argument a pointer to z. The procedure considers the three cases shown in Figure 12.4. If z has no children, we modify its parent p[z] to replace z with NIL as its child. If the node has only a single child, we "splice out" z by making a new link between its child and its parent. Finally, if the node has two children, we splice out z's successor y, which has no left child (see Exercise 12.2-5) and replace z's key and satellite data with y's key and satellite data.
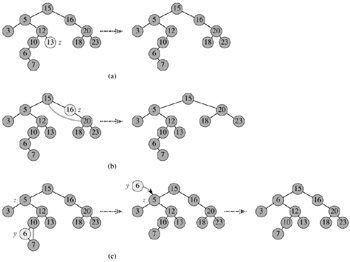
The code for TREE-DELETE organizes these three cases a little differently.
TREE-DELETE(T, z) 1 if left[z] = NIL or right[z] = NIL 2 then y ← z 3 else y ← TREE-SUCCESSOR(z) 4 if left[y] ≠ NIL 5 then x ← left[y] 6 else x ← right[y] 7 if x ≠ NIL 8 then p[x] ← p[y] 9 if p[y] = NIL 10 then root[T] ← x 11 else if y = left[p[y]] 12 then left[p[y]] ← x 13 else right[p[y]] ← x 14 if y ≠ z 15 then key[z] ← key[y] 16 copy y's satellite data into z 17 return y
In lines 1-3, the algorithm determines a node y to splice out. The node y is either the input node z (if z has at most 1 child) or the successor of z (if z has two children). Then, in lines 4-6, x is set to the non-NIL child of y, or to NIL if y has no children. The node y is spliced out in lines 7-13 by modifying pointers in p[y] and x. Splicing out y is somewhat complicated by the need for proper handling of the boundary conditions, which occur when x = NIL or when y is the root. Finally, in lines 14-16, if the successor of z was the node spliced out, y's key and satellite data are moved to z, overwriting the previous key and satellite data. The node y is returned in line 17 so that the calling procedure can recycle it via the free list. The procedure runs in O(h) time on a tree of height h.
In summary, we have proved the following theorem.
The dynamic-set operations INSERT and DELETE can be made to run in O(h) time on a binary search tree of height h.
Suppose that a binary search tree is constructed by repeatedly inserting distinct values into the tree. Argue that the number of nodes examined in searching for a value in the tree is one plus the number of nodes examined when the value was first inserted into the tree.
We can sort a given set of n numbers by first building a binary search tree containing these numbers (using TREE-INSERT repeatedly to insert the numbers one by one) and then printing the numbers by an inorder tree walk. What are the worst-case and best-case running times for this sorting algorithm?
Suppose that another data structure contains a pointer to a node y in a binary search tree, and suppose that y's predecessor z is deleted from the tree by the procedure TREE-DELETE. What problem can arise? How can TREE-DELETE be rewritten to solve this problem?
Is the operation of deletion "commutative" in the sense that deleting x and then y from a binary search tree leaves the same tree as deleting y and then x? Argue why it is or give a counterexample.
When node z in TREE-DELETE has two children, we could splice out its predecessor rather than its successor. Some have argued that a fair strategy, giving equal priority to predecessor and successor, yields better empirical performance. How might TREE-DELETE be changed to implement such a fair strategy?
| < Day Day Up > |