13.2 Rotations

The search-tree operations TREE-INSERT and TREE-DELETE, when run on a red-black tree with n keys, take O(lg n) time. Because they modify the tree, the result may violate the red-black properties enumerated in Section 13.1. To restore these properties, we must change the colors of some of the nodes in the tree and also change the pointer structure.

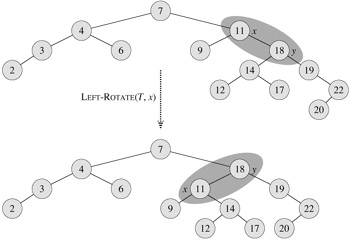
We change the pointer structure through rotation, which is a local operation in a search tree that preserves the binary-search-tree property. Figure 13.2 shows the two kinds of rotations: left rotations and right rotations. When we do a left rotation on a node x, we assume that its right child y is not nil[T]; x may be any node in the tree whose right child is not nil[T]. The left rotation "pivots" around the link from x to y. It makes y the new root of the subtree, with x as y's left child and y's left child as x's right child.

Figure 13.2: The rotation operations on a binary search tree. The operation LEFT-ROTATE(T, x) transforms the configuration of the two nodes on the left into the configuration on the right by changing a constant number of pointers. The configuration on the right can be transformed into the configuration on the left by the inverse operation RIGHT-ROTATE(T, y). The letters α, β, and γ represent arbitrary subtrees. A rotation operation preserves the binary-search-tree property: the keys in α precede key[x], which precedes the keys in β, which precede key[y], which precedes the keys in γ.

The pseudocode for LEFT-ROTATE assumes that right[x] ≠ nil[T] and that the root's parent is nil[T].

LEFT-ROTATE(T, x)
 1  y ← right[x]            ▹ Set y.
 2  right[x] ← left[y]      ▹ Turn y's left subtree into x's right subtree.
 3  p[left[y]] ← x
 4  p[y] ← p[x]             ▹ Link x's parent to y.
 5  if p[x] = nil[T]
 6     then root[T] ← y
 7     else if x = left[p[x]]
 8             then left[p[x]] ← y
 9             else right[p[x]] ← y
10  left[y] ← x             ▹ Put x on y's left.
11  p[x] ← y

Figure 13.3 shows how LEFT-ROTATE operates. The code for RIGHT-ROTATE is symmetric. Both LEFT-ROTATE and RIGHT-ROTATE run in O(1) time. Only pointers are changed by a rotation; all other fields in a node remain the same.

Figure 13.3: An example of how the procedure LEFT-ROTATE(T, x) modifies a binary search tree. Inorder tree walks of the input tree and the modified tree produce the same listing of key values.

Exercises 13.2-1

Write pseudocode for RIGHT-ROTATE.

Exercises 13.2-2

Argue that in every n-node binary search tree, there are exactly n - 1 possible rotations.

Exercises 13.2-3

Let a, b, and c be arbitrary nodes in subtrees α, β, and γ, respectively, in the left tree of Figure 13.2. How do the depths of a, b, and c change when a left rotation is performed on node x in the figure?

Exercises 13.2-4

Show that any arbitrary n-node binary search tree can be transformed into any other arbitrary n-node binary search tree using O(n) rotations. (Hint: First show that at most n - 1 right rotations suffice to transform the tree into a right-going chain.)

Exercises 13.2-5: ⋆

We say that a binary search tree T₁ can be right-converted to binary search tree T₂ if it is possible to obtain T₂ from T₁ via a series of calls to RIGHT-ROTATE. Give an example of two trees T₁ and T₂ such that T₁ cannot be right-converted to T₂. Then show that if a tree T₁ can be right-converted to T₂, it can be right-converted using O(n²) calls to RIGHT-ROTATE.