| < Day Day Up > |
Insertion of a node into an n-node red-black tree can be accomplished in O(lg n) time. We use a slightly modified version of the TREE-INSERT procedure (Section 12.3) to insert node z into the tree T as if it were an ordinary binary search tree, and then we color z red. To guarantee that the red-black properties are pre- served, we then call an auxiliary procedure RB-INSERT-FIXUP to recolor nodes and perform rotations. The call RB-INSERT(T, z) inserts node z, whose key field is assumed to have already been filled in, into the red-black tree T.
RB-INSERT(T, z) 1 y ← nil[T] 2 x ← root[T] 3 while x ≠ nil[T] 4 do y ← x 5 if key[z] < key[x] 6 then x ← left[x] 7 else x ← right[x] 8 p[z] ← y 9 if y = nil[T] 10 then root[T] ← z 11 else if key[z] < key[y] 12 then left[y] ← z 13 else right[y] ← z 14 left[z] ← nil[T] 15 right[z] ← nil[T] 16 color[z] ← RED 17 RB-INSERT-FIXUP(T, z)
There are four differences between the procedures TREE-INSERT and RB-INSERT. First, all instances of NIL in TREE-INSERT are replaced by nil[T]. Second, we set left[z] and right[z] to nil[T] in lines 14-15 of RB-INSERT, in order to maintain the proper tree structure. Third, we color z red in line 16. Fourth, because coloring z red may cause a violation of one of the red-black properties, we call RB-INSERT-FIXUP(T, z) in line 17 of RB-INSERT to restore the red-black properties.
RB-INSERT-FIXUP(T, z) 1 while color[p[z]] = RED 2 do if p[z] = left[p[p[z]]] 3 then y ← right[p[p[z]]] 4 if color[y] = RED 5 then color[p[z]] ← BLACK ▹ Case 1 6 color[y] ← BLACK ▹ Case 1 7 color[p[p[z]]] ← RED ▹ Case 1 8 z ← p[p[z]] ▹ Case 1 9 else if z = right[p[z]] 10 then z ← p[z] ▹ Case 2 11 LEFT-ROTATE(T, z) ▹ Case 2 12 color[p[z]] ← BLACK ▹ Case 3 13 color[p[p[z]]] ← RED ▹ Case 3 14 RIGHT-ROTATE(T, p[p[z]]) ▹ Case 3 15 else (same as then clause with "right" and "left" exchanged) 16 color[root[T]] ← BLACK
To understand how RB-INSERT-FIXUP works, we shall break our examination of the code into three major steps. First, we shall determine what violations of the red-black properties are introduced in RB-INSERT when the node z is inserted and colored red. Second, we shall examine the overall goal of the while loop in lines 1-15. Finally, we shall explore each of the three cases[1] into which the while loop is broken and see how they accomplish the goal. Figure 13.4 shows how RB-INSERT-FIXUP operates on a sample red-black tree.
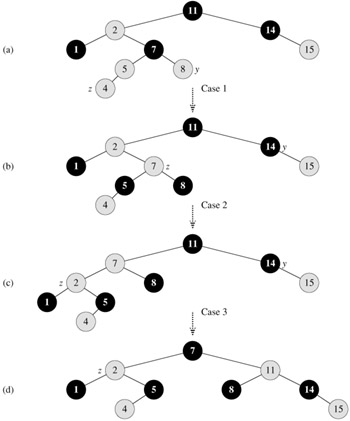
Which of the red-black properties can be violated upon the call to RB-INSERT-FIXUP? Property 1 certainly continues to hold, as does property 3, since both children of the newly inserted red node are the sentinel nil[T]. Property 5, which says that the number of black nodes is the same on every path from a given node, is satisfied as well, because node z replaces the (black) sentinel, and node z is red with sentinel children. Thus, the only properties that might be violated are property 2, which requires the root to be black, and property 4, which says that a red node cannot have a red child. Both possible violations are due to z being colored red. Property 2 is violated if z is the root, and property 4 is violated if z's parent is red. Figure 13.4(a) shows a violation of property 4 after the node z has been inserted.
The while loop in lines 1-15 maintains the following three-part invariant:
At the start of each iteration of the loop,
Node z is red.
If p[z] is the root, then p[z] is black.
If there is a violation of the red-black properties, there is at most one violation, and it is of either property 2 or property 4. If there is a violation of property 2, it occurs because z is the root and is red. If there is a violation of property 4, it occurs because both z and p[z] are red.
Part (c), which deals with violations of red-black properties, is more central to showing that RB-INSERT-FIXUP restores the red-black properties than parts (a) and (b), which we use along the way to understand situations in the code. Because we will be focusing on node z and nodes near it in the tree, it is helpful to know from part (a) that z is red. We shall use part (b) to show that the node p[p[z]] exists when we reference it in lines 2, 3, 7, 8, 13, and 14.
Recall that we need to show that a loop invariant is true prior to the first iteration of the loop, that each iteration maintains the loop invariant, and that the loop invariant gives us a useful property at loop termination.
We start with the initialization and termination arguments. Then, as we examine how the body of the loop works in more detail, we shall argue that the loop maintains the invariant upon each iteration. Along the way, we will also demonstrate that there are two possible outcomes of each iteration of the loop: the pointer z moves up the tree, or some rotations are performed and the loop terminates.
Initialization: Prior to the first iteration of the loop, we started with a red-black tree with no violations, and we added a red node z. We show that each part of the invariant holds at the time RB-INSERT-FIXUP is called:
When RB-INSERT-FIXUP is called, z is the red node that was added.
If p[z] is the root, then p[z] started out black and did not change prior to the call of RB-INSERT-FIXUP.
We have already seen that properties 1, 3, and 5 hold when RB-INSERT-FIXUP is called.
If there is a violation of property 2, then the red root must be the newly added node z, which is the only internal node in the tree. Because the parent and both children of z are the sentinel, which is black, there is not also a violation of property 4. Thus, this violation of property 2 is the only violation of red-black properties in the entire tree.
If there is a violation of property 4, then because the children of node z are black sentinels and the tree had no other violations prior to z being added, the violation must be because both z and p[z] are red. Moreover, there are no other violations of red-black properties.
Termination: When the loop terminates, it does so because p[z] is black. (If z is the root, then p[z] is the sentinel nil[T], which is black.) Thus, there is no violation of property 4 at loop termination. By the loop invariant, the only property that might fail to hold is property 2. Line 16 restores this property, too, so that when RB-INSERT-FIXUP terminates, all the red-black properties hold.
Maintenance: There are actually six cases to consider in the while loop, but three of them are symmetric to the other three, depending on whether z's parent p[z] is a left child or a right child of z's grandparent p[p[z]], which is determined in line 2. We have given the code only for the situation in which p[z] is a left child. The node p[p[z]] exists, since by part (b) of the loop invariant, if p[z] is the root, then p[z] is black. Since we enter a loop iteration only if p[z] is red, we know that p[z] cannot be the root. Hence, p[p[z]] exists.
Case 1 is distinguished from cases 2 and 3 by the color of z's parent's sibling, or "uncle." Line 3 makes y point to z's uncle right[p[p[z]]], and a test is made in line 4. If y is red, then case 1 is executed. Otherwise, control passes to cases 2 and 3. In all three cases, z's grandparent p[p[z]] is black, since its parent p[z] is red, and property 4 is violated only between z and p[z].
Figure 13.5 shows the situation for case 1 (lines 5-8). Case 1 is executed when both p[z] and y are red. Since p[p[z]] is black, we can color both p[z] and y black, thereby fixing the problem of z and p[z] both being red, and color p[p[z]] red, thereby maintaining property 5. We then repeat the while loop with p[p[z]] as the new node z. The pointer z moves up two levels in the tree.
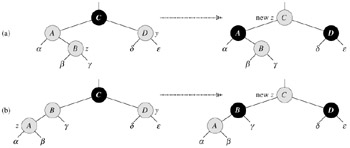
Now we show that case 1 maintains the loop invariant at the start of the next iteration. We use z to denote node z in the current iteration, and z′ p[p[z]] to denote the node z at the test in line 1 upon the next iteration.
Because this iteration colors p[p[z]] red, node z′ is red at the start of the next iteration.
The node p[z′] is p[p[p[z]]] in this iteration, and the color of this node does not change. If this node is the root, it was black prior to this iteration, and it remains black at the start of the next iteration.
We have already argued that case 1 maintains property 5, and it clearly does not introduce a violation of properties 1 or 3.
If node z′ is the root at the start of the next iteration, then case 1 corrected the lone violation of property 4 in this iteration. Since z′ is red and it is the root, property 2 becomes the only one that is violated, and this violation is due to z′.
If node z′ is not the root at the start of the next iteration, then case 1 has not created a violation of property 2. Case 1 corrected the lone violation of property 4 that existed at the start of this iteration. It then made z′ red and left p[z′] alone. If p[z′] was black, there is no violation of property 4. If p[z′] was red, coloring z′ red created one violation of property 4 between z′ and p[z′].
In cases 2 and 3, the color of z's uncle y is black. The two cases are distinguished by whether z is a right or left child of p[z]. Lines 10-11 constitute case 2, which is shown in Figure 13.6 together with case 3. In case 2, node z is a right child of its parent. We immediately use a left rotation to transform the situation into case 3 (lines 12-14), in which node z is a left child. Because both z and p[z] are red, the rotation affects neither the black-height of nodes nor property 5. Whether we enter case 3 directly or through case 2, z's uncle y is black, since otherwise we would have executed case 1. Additionally, the node p[p[z]] exists, since we have argued that this node existed at the time that lines 2 and 3 were executed, and after moving z up one level in line 10 and then down one level in line 11, the identity of p[p[z]] remains unchanged. In case 3, we execute some color changes and a right rotation, which preserve property 5, and then, since we no longer have two red nodes in a row, we are done. The body of the while loop is not executed another time, since p[z] is now black.
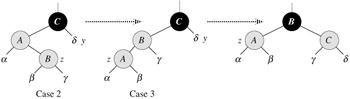
Now we show that cases 2 and 3 maintain the loop invariant. (As we have just argued, p[z] will be black upon the next test in line 1, and the loop body will not execute again.)
Case 2 makes z point to p[z], which is red. No further change to z or its color occurs in cases 2 and 3.
Case 3 makes p[z] black, so that if p[z] is the root at the start of the next iteration, it is black.
As in case 1, properties 1, 3, and 5 are maintained in cases 2 and 3.
Since node z is not the root in cases 2 and 3, we know that there is no violation of property 2. Cases 2 and 3 do not introduce a violation of property 2, since the only node that is made red becomes a child of a black node by the rotation in case 3.
Cases 2 and 3 correct the lone violation of property 4, and they do not intro- duce another violation.
Having shown that each iteration of the loop maintains the invariant, we have shown that RB-INSERT-FIXUP correctly restores the red-black properties.
What is the running time of RB-INSERT? Since the height of a red-black tree on n nodes is O(lg n), lines 1-16 of RB-INSERT take O(lg n) time. In RB-INSERT- FIXUP, the while loop repeats only if case 1 is executed, and then the pointer z moves two levels up the tree. The total number of times the while loop can be executed is therefore O(lg n). Thus, RB-INSERT takes a total of O(lg n) time. Interestingly, it never performs more than two rotations, since the while loop terminates if case 2 or case 3 is executed.
In line 16 of RB-INSERT, we set the color of the newly inserted node z to red. Notice that if we had chosen to set z's color to black, then property 4 of a red-black tree would not be violated. Why didn't we choose to set z's color to black?
Show the red-black trees that result after successively inserting the keys 41, 38, 31, 12, 19, 8 into an initially empty red-black tree.
Suppose that the black-height of each of the subtrees α, β, γ, δ, ε in Figures 13.5 and 13.6 is k. Label each node in each figure with its black-height to verify that property 5 is preserved by the indicated transformation.
Professor Teach is concerned that RB-INSERT-FIXUP might set color[nil[T]] to RED, in which case the test in line 1 would not cause the loop to terminate when z is the root. Show that the professor's concern is unfounded by arguing that RB-INSERT-FIXUP never sets color[nil[T]] to RED.
[1]Case 2 falls through into case 3, and so these two cases are not mutually exclusive.
| < Day Day Up > |