Prefix codes

We consider here only codes in which no codeword is also a prefix of some other codeword. Such codes are called prefix codes.^[2] It is possible to show (although we won't do so here) that the optimal data compression achievable by a character code can always be achieved with a prefix code, so there is no loss of generality in restricting attention to prefix codes.

Encoding is always simple for any binary character code; we just concatenate the codewords representing each character of the file. For example, with the variable-length prefix code of Figure 16.3, we code the 3-character file abc as 0·101·100 = 0101100, where we use "·" to denote concatenation.

Prefix codes are desirable because they simplify decoding. Since no codeword is a prefix of any other, the codeword that begins an encoded file is unambiguous. We can simply identify the initial codeword, translate it back to the original character, and repeat the decoding process on the remainder of the encoded file. In our example, the string 001011101 parses uniquely as 0 · 0 · 101 · 1101, which decodes to aabe.

The decoding process needs a convenient representation for the prefix code so that the initial codeword can be easily picked off. A binary tree whose leaves are the given characters provides one such representation. We interpret the binary codeword for a character as the path from the root to that character, where 0 means "go to the left child" and 1 means "go to the right child." Figure 16.4 shows the trees for the two codes of our example. Note that these are not binary search trees, since the leaves need not appear in sorted order and internal nodes do not contain character keys.

Figure 16.4: Trees corresponding to the coding schemes in Figure 16.3. Each leaf is labeled with a character and its frequency of occurrence. Each internal node is labeled with the sum of the frequencies of the leaves in its subtree. (a) The tree corresponding to the fixed-length code a = 000, ..., f = 101. (b) The tree corresponding to the optimal prefix code a = 0, b = 101, ..., f = 1100.

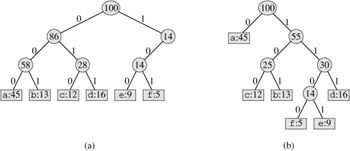
An optimal code for a file is always represented by a full binary tree, in which every nonleaf node has two children (see Exercise 16.3-1). The fixed-length code in our example is not optimal since its tree, shown in Figure 16.4(a), is not a full binary tree: there are codewords beginning 10..., but none beginning 11.... Since we can now restrict our attention to full binary trees, we can say that if C is the alphabet from which the characters are drawn and all character frequencies are positive, then the tree for an optimal prefix code has exactly |C| leaves, one for each letter of the alphabet, and exactly |C| - 1 internal nodes (see Exercise B.5-3).

Given a tree T corresponding to a prefix code, it is a simple matter to compute the number of bits required to encode a file. For each character c in the alphabet C, let f (c) denote the frequency of c in the file and let d_T(c) denote the depth of c's leaf in the tree. Note that d_T(c) is also the length of the codeword for character c. The number of bits required to encode a file is thus

(16.5)

which we define as the cost of the tree T.

Constructing a Huffman code

Huffman invented a greedy algorithm that constructs an optimal prefix code called a Huffman code. Keeping in line with our observations in Section 16.2, its proof of correctness relies on the greedy-choice property and optimal substructure. Rather than demonstrating that these properties hold and then developing pseudocode, we present the pseudocode first. Doing so will help clarify how the algorithm makes greedy choices.

In the pseudocode that follows, we assume that C is a set of n characters and that each character c ∈ C is an object with a defined frequency f [c]. The algorithm builds the tree T corresponding to the optimal code in a bottom-up manner. It begins with a set of |C| leaves and performs a sequence of |C| - 1 "merging" operations to create the final tree. A min-priority queue Q, keyed on f , is used to identify the two least-frequent objects to merge together. The result of the merger of two objects is a new object whose frequency is the sum of the frequencies of the two objects that were merged.

HUFFMAN(C)
1  n ← |C|
2  Q ← C
3  for i 1 to n - 1
4       do allocate a new node z
5          left[z] ← x ← EXTRACT-MIN (Q)
6          right[z] ← y ← EXTRACT-MIN (Q)
7          f [z] ← f [x] + f [y]
8          INSERT(Q, z)
9  return EXTRACT-MIN(Q)   ▹Return the root of the tree.

For our example, Huffman's algorithm proceeds as shown in Figure 16.5. Since there are 6 letters in the alphabet, the initial queue size is n = 6, and 5 merge steps are required to build the tree. The final tree represents the optimal prefix code. The codeword for a letter is the sequence of edge labels on the path from the root to the letter.

Figure 16.5: The steps of Huffman's algorithm for the frequencies given in Figure 16.3. Each part shows the contents of the queue sorted into increasing order by frequency. At each step, the two trees with lowest frequencies are merged. Leaves are shown as rectangles containing a character and its frequency. Internal nodes are shown as circles containing the sum of the frequencies of its children. An edge connecting an internal node with its children is labeled 0 if it is an edge to a left child and 1 if it is an edge to a right child. The codeword for a letter is the sequence of labels on the edges connecting the root to the leaf for that letter. (a) The initial set of n = 6 nodes, one for each letter. (b)-(e) Intermediate stages. (f) The final tree.

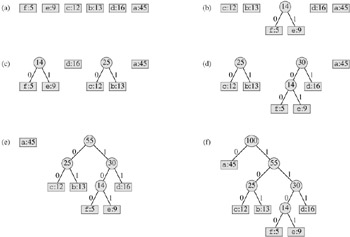
Line 2 initializes the min-priority queue Q with the characters in C. The for loop in lines 3-8 repeatedly extracts the two nodes x and y of lowest frequency from the queue, and replaces them in the queue with a new node z representing their merger. The frequency of z is computed as the sum of the frequencies of x and y in line 7. The node z has x as its left child and y as its right child. (This order is arbitrary; switching the left and right child of any node yields a different code of the same cost.) After n - 1 mergers, the one node left in the queue-the root of the code tree-is returned in line 9.

The analysis of the running time of Huffman's algorithm assumes that Q is implemented as a binary min-heap (see Chapter 6). For a set C of n characters, the initialization of Q in line 2 can be performed in O (n) time using the BUILD-MIN-HEAP procedure in Section 6.3. The for loop in lines 3-8 is executed exactly n - 1 times, and since each heap operation requires time O (lg n), the loop contributes O (n lg n) to the running time. Thus, the total running time of HUFFMAN on a set of n characters is O (n lg n).

Correctness of Huffman's algorithm

To prove that the greedy algorithm HUFFMAN is correct, we show that the problem of determining an optimal prefix code exhibits the greedy-choice and optimal-substructure properties. The next lemma shows that the greedy-choice property holds.

Lemma 16.2

Let C be an alphabet in which each character c ∈ C has frequency f [c]. Let x and y be two characters in C having the lowest frequencies. Then there exists an optimal prefix code for C in which the codewords for x and y have the same length and differ only in the last bit.

Proof The idea of the proof is to take the tree T representing an arbitrary optimal prefix code and modify it to make a tree representing another optimal prefix code such that the characters x and y appear as sibling leaves of maximum depth in the new tree. If we can do this, then their codewords will have the same length and differ only in the last bit.

Let a and b be two characters that are sibling leaves of maximum depth in T. Without loss of generality, we assume that f[a] ≤ f[b] and f[x] ≤ f[y]. Since f[x] and f[y] are the two lowest leaf frequencies, in order, and f[a] and f[b] are two arbitrary frequencies, in order, we have f [x] ≤ f[a] and f[y] ≤ f[b]. As shown in Figure 16.6, we exchange the positions in T of a and x to produce a tree T′, and then we exchange the positions in T′ of b and y to produce a tree T′. By equation (16.5), the difference in cost between T and T′ is

Figure 16.6: An illustration of the key step in the proof of Lemma 16.2. In the optimal tree T, leaves a and b are two of the deepest leaves and are siblings. Leaves x and y are the two leaves that Huffman's algorithm merges together first; they appear in arbitrary positions in T . Leaves a and x are swapped to obtain tree T′. Then, leaves b and y are swapped to obtain tree T′. Since each swap does not increase the cost, the resulting tree T′ is also an optimal tree.

because both f[a] - f[x] and d_T (a) - d_T (x) are nonnegative. More specifically, f[a] - f[x] is nonnegative because x is a minimum-frequency leaf, and d_T (a) - d_T (x) is nonnegative because a is a leaf of maximum depth in T. Similarly, exchanging y and b does not increase the cost, and so B(T′) - B(T′) is nonnegative. Therefore, B(T′) ≤ B(T), and since T is optimal, B(T) ≤ B(T′), which implies B(T′) = B(T). Thus, T′ is an optimal tree in which x and y appear as sibling leaves of maximum depth, from which the lemma follows.

Lemma 16.2 implies that the process of building up an optimal tree by mergers can, without loss of generality, begin with the greedy choice of merging together those two characters of lowest frequency. Why is this a greedy choice? We can view the cost of a single merger as being the sum of the frequencies of the two items being merged. Exercise 16.3-3 shows that the total cost of the tree constructed is the sum of the costs of its mergers. Of all possible mergers at each step, HUFFMAN chooses the one that incurs the least cost.

The next lemma shows that the problem of constructing optimal prefix codes has the optimal-substructure property.

Lemma 16.3

Let C be a given alphabet with frequency f[c] defined for each character c ∈ C. Let x and y be two characters in C with minimum frequency. Let C′ be the alphabet C with characters x, y removed and (new) character z added, so that C′ = C - {x, y} ∪ {z}; define f for C′ as for C, except that f[z] = f[x] + f[y]. Let T′ be any tree representing an optimal prefix code for the alphabet C′. Then the tree T, obtained from T′ by replacing the leaf node for z with an internal node having x and y as children, represents an optimal prefix code for the alphabet C.

Proof We first show that the cost B(T) of tree T can be expressed in terms of the cost B(T′) of tree T′ by considering the component costs in equation (16.5). For each c ∈ C - {x, y}, we have d_T (c) = d_T′ (c), and hence f[c]d_T(c) = f[c]d_′(c). Since d_T (x) = d_T (y) = d_′(z) + 1, we have

f[x]dT (x) + f[y]dT (y)	=	(f[x] + f[y])(d′ (z) + 1)
	=	f[z]d′(z) + (f[x] + f[y]),

from which we conclude that

B(T) = B(T′) + f[x] + f[y]

or, equivalently,

B(T′) = B(T) - f[x] - f[y].

We now prove the lemma by contradiction. Suppose that T does not represent an optimal prefix code for C. Then there exists a tree T′ such that B(T′) < B(T). Without loss of generality (by Lemma 16.2), T′ has x and y as siblings. Let T′′′ be the tree T′ with the common parent of x and y replaced by a leaf z with frequency f[z] = f[x] + f[y]. Then

B(T‴)	=	B(T′) - f[x] - f[y]
	<	B(T) - f[x] - f[y]
	=	B(T′),

yielding a contradiction to the assumption that T′ represents an optimal prefix code for C′. Thus, T must represent an optimal prefix code for the alphabet C.

Theorem 16.4

Procedure HUFFMAN produces an optimal prefix code.

Proof Immediate from Lemmas 16.2 and 16.3.

Exercises 16.3-1

Prove that a binary tree that is not full cannot correspond to an optimal prefix code.

Exercises 16.3-2

What is an optimal Huffman code for the following set of frequencies, based on the first 8 Fibonacci numbers?

a:1 b:1 c:2 d:3 e:5 f:8 g:13 h:21

Can you generalize your answer to find the optimal code when the frequencies are the first n Fibonacci numbers?

Exercises 16.3-3

Prove that the total cost of a tree for a code can also be computed as the sum, over all internal nodes, of the combined frequencies of the two children of the node.

Exercises 16.3-4

Prove that if we order the characters in an alphabet so that their frequencies are monotonically decreasing, then there exists an optimal code whose codeword lengths are monotonically increasing.

Exercises 16.3-5

Suppose we have an optimal prefix code on a set C = {0, 1, ..., n - 1} of characters and we wish to transmit this code using as few bits as possible. Show how to represent any optimal prefix code on C using only 2n - 1 + n ⌈lg n⌉ bits. (Hint: Use 2n - 1 bits to specify the structure of the tree, as discovered by a walk of the tree.)

Exercises 16.3-6

Generalize Huffman's algorithm to ternary codewords (i.e., codewords using the symbols 0, 1, and 2), and prove that it yields optimal ternary codes.

Exercises 16.3-7

Suppose a data file contains a sequence of 8-bit characters such that all 256 characters are about as common: the maximum character frequency is less than twice the minimum character frequency. Prove that Huffman coding in this case is no more efficient than using an ordinary 8-bit fixed-length code.

Exercises 16.3-8

Show that no compression scheme can expect to compress a file of randomly chosen 8-bit characters by even a single bit. (Hint: Compare the number of files with the number of possible encoded files.)