Decreasing a key

In the following pseudocode for the operation FIB-HEAP-DECREASE-KEY, we assume as before that removing a node from a linked list does not change any of the structural fields in the removed node.

FIB-HEAP-DECREASE-KEY(H, x, k)
1  if k > key[x]
2     then error "new key is greater than current key"
3  key[x] ← k
4  y ← p[x]
5  if y ≠ NIL and key[x] < key[y]
6     then CUT(H, x, y)
7          CASCADING-CUT(H, y)
8  if key[x] < key[min[H]]
9      then min[H] ← x

CUT(H, x, y)
1 remove x from the child list of y, decrementing degree[y]
2 add x to the root list of H
3 p[x] ← NIL
4 mark[x] ← FALSE

CASCADING-CUT(H, y)
1 z ← p[y]
2 if z ≠ NIL
3    then if mark[y] = FALSE
4            then mark[y] ← TRUE
5            else CUT(H, y, z)
6                 CASCADING-CUT(H, z)

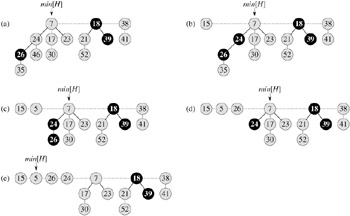
The FIB-HEAP-DECREASE-KEY procedure works as follows. Lines 1-3 ensure that the new key is no greater than the current key of x and then assign the new key to x. If x is a root or if key[x] ≥ key[y], where y is x's parent, then no structural changes need occur, since min-heap order has not been violated. Lines 4-5 test for this condition.

If min-heap order has been violated, many changes may occur. We start by cutting x in line 6. The CUT procedure "cuts" the link between x and its parent y, making x a root.

We use the mark fields to obtain the desired time bounds. They record a little piece of the history of each node. Suppose that the following events have happened to node x:

1. at some time, x was a root,

2. then x was linked to another node,

3. then two children of x were removed by cuts.

As soon as the second child has been lost, we cut x from its parent, making it a new root. The field mark[x] is TRUE if steps 1 and 2 have occurred and one child of x has been cut. The CUT procedure, therefore, clears mark[x] in line 4, since it performs step 1. (We can now see why line 3 of FIB-HEAP-LINK clears mark[y]: node y is being linked to another node, and so step 2 is being performed. The next time a child of y is cut, mark[y] will be set to TRUE.)

We are not yet done, because x might be the second child cut from its parent y since the time that y was linked to another node. Therefore, line 7 of FIB-HEAP-DECREASE-KEY performs a cascading-cut operation on y. If y is a root, then the test in line 2 of CASCADING-CUT causes the procedure to just return. If y is unmarked, the procedure marks it in line 4, since its first child has just been cut, and returns. If y is marked, however, it has just lost its second child; y is cut in line 5, and CASCADING-CUT calls itself recursively in line 6 on y's parent z. The CASCADING-CUT procedure recurses its way up the tree until either a root or an unmarked node is found.

Once all the cascading cuts have occurred, lines 8-9 of FIB-HEAP-DECREASE-KEY finish up by updating min[H] if necessary. The only node whose key changed was the node x whose key decreased. Thus, the new minimum node is either the original minimum node or node x.

Figure 20.4 shows the execution of two calls of FIB-HEAP-DECREASE-KEY, starting with the Fibonacci heap shown in Figure 20.4(a). The first call, shown in Figure 20.4(b), involves no cascading cuts. The second call, shown in Figures 20.4(c)-(e), invokes two cascading cuts.

Figure 20.4: Two calls of FIB-HEAP-DECREASE-KEY. (a) The initial Fibonacci heap. (b) The node with key 46 has its key decreased to 15. The node becomes a root, and its parent (with key 24), which had previously been unmarked, becomes marked. (c)-(e) The node with key 35 has its key decreased to 5. In part (c), the node, now with key 5, becomes a root. Its parent, with key 26, is marked, so a cascading cut occurs. The node with key 26 is cut from its parent and made an unmarked root in (d). Another cascading cut occurs, since the node with key 24 is marked as well. This node is cut from its parent and made an unmarked root in part (e). The cascading cuts stop at this point, since the node with key 7 is a root. (Even if this node were not a root, the cascading cuts would stop, since it is unmarked.) The result of the FIB-HEAP-DECREASE-KEY operation is shown in part (e), with min[H] pointing to the new minimum node.

We shall now show that the amortized cost of FIB-HEAP-DECREASE-KEY is only O(1). We start by determining its actual cost. The FIB-HEAP-DECREASE-KEY procedure takes O(1) time, plus the time to perform the cascading cuts. Suppose that CASCADING-CUT is recursively called c times from a given invocation of FIB-HEAP-DECREASE-KEY. Each call of CASCADING-CUT takes O(1) time exclusive of recursive calls. Thus, the actual cost of FIB-HEAP-DECREASE-KEY, including all recursive calls, is O(c).

We next compute the change in potential. Let H denote the Fibonacci heap just prior to the FIB-HEAP-DECREASE-KEY operation. Each recursive call of CASCADING-CUT, except for the last one, cuts a marked node and clears the mark bit. Afterward, there are t(H)+c trees (the original t(H) trees, c-1 trees produced by cascading cuts, and the tree rooted at x) and at most m(H) - c +2 marked nodes (c-1 were unmarked by cascading cuts and the last call of CASCADING-CUT may have marked a node). The change in potential is therefore at most

((t(H) + c) + 2(m(H) - c + 2)) - (t(H) + 2m(H)) = 4 - c.

Thus, the amortized cost of FIB-HEAP-DECREASE-KEY is at most

O(c) + 4 - c = O(1),

since we can scale up the units of potential to dominate the constant hidden in O(c).

You can now see why the potential function was defined to include a term that is twice the number of marked nodes. When a marked node y is cut by a cascading cut, its mark bit is cleared, so the potential is reduced by 2. One unit of potential pays for the cut and the clearing of the mark bit, and the other unit compensates for the unit increase in potential due to node y becoming a root.

Deleting a node

It is easy to delete a node from an n-node Fibonacci heap in O(D(n)) amortized time, as is done by the following pseudocode. We assume that there is no key value of -∞ currently in the Fibonacci heap.

FIB-HEAP-DELETE(H, x)
1 FIB-HEAP-DECREASE-KEY(H, x, -∞)
2 FIB-HEAP-EXTRACT-MIN(H)

FIB-HEAP-DELETE is analogous to BINOMIAL-HEAP-DELETE. It makes x become the minimum node in the Fibonacci heap by giving it a uniquely small key of -∞. Node x is then removed from the Fibonacci heap by the FIB-HEAP-EXTRACT-MIN procedure. The amortized time of FIB-HEAP-DELETE is the sum of the O(1) amortized time of FIB-HEAP-DECREASE-KEY and the O(D(n)) amortized time of FIB-HEAP-EXTRACT-MIN. Since we shall see in Section 20.4 that D(n) = O(lg n), the amortized time of FIB-HEAP-DELETE is O(lg n).

Exercises 20.3-1

Suppose that a root x in a Fibonacci heap is marked. Explain how x came to be a marked root. Argue that it doesn't matter to the analysis that x is marked, even though it is not a root that was first linked to another node and then lost one child.

Exercises 20.3-2

Justify the O(1) amortized time of FIB-HEAP-DECREASE-KEY as an average cost per operation by using aggregate analysis.