Creating a new Fibonacci heap

To make an empty Fibonacci heap, the MAKE-FIB-HEAP procedure allocates and returns the Fibonacci heap object H , where n[H ] = 0 and min[H ] = NIL; there are no trees in H . Because t(H) = 0 and m(H) = 0, the potential of the empty Fibonacci heap is Φ(H) = 0. The amortized cost of MAKE-FIB-HEAP is thus equal to its O(1) actual cost.

Inserting a node

The following procedure inserts node x into Fibonacci heap H , assuming that the node has already been allocated and that key[x] has already been filled in.

FIB-HEAP-INSERT(H, x)
 1  degree[x] ← 0
 2  p[x] ← NIL
 3  child[x] ← NIL
 4  left[x] ← x
 5  right[x] ← x
 6  mark[x] ← FALSE
 7  concatenate the root list containing x with root list H
 8  if min[H] = NIL or key[x] < key[min[H]]
 9     then min[H] ← x
10  n[H] ← n[H] + 1

After lines 1-6 initialize the structural fields of node x, making it its own circular, doubly linked list, line 7 adds x to the root list of H in O(1) actual time. Thus, node x becomes a single-node min-heap-ordered tree, and thus an unordered binomial tree, in the Fibonacci heap. It has no children and is unmarked. Lines 8-9 then update the pointer to the minimum node of Fibonacci heap H if necessary. Finally, line 10 increments n[H] to reflect the addition of the new node. Figure 20.2 shows a node with key 21 inserted into the Fibonacci heap of Figure 20.1.

Figure 20.2: Inserting a node into a Fibonacci heap. (a) A Fibonacci heap H. (b) Fibonacci heap H after the node with key 21 has been inserted. The node becomes its own min-heap-ordered tree and is then added to the root list, becoming the left sibling of the root.

Unlike the BINOMIAL-HEAP-INSERT procedure, FIB-HEAP-INSERT makes no attempt to consolidate the trees within the Fibonacci heap. If k consecutive FIB-HEAP-INSERT operations occur, then k single-node trees are added to the root list.

To determine the amortized cost of FIB-HEAP-INSERT, let H be the input Fibonacci heap and H′ be the resulting Fibonacci heap. Then, t(H′) = t(H)+1 and m(H′) = m(H), and the increase in potential is

((t(H) + 1) + 2 m(H)) - (t(H) + 2 m(H)) = 1.

Since the actual cost is O(1), the amortized cost is O(1) + 1 = O(1).

Finding the minimum node

The minimum node of a Fibonacci heap H is given by the pointer min[H ], so we can find the minimum node in O(1) actual time. Because the potential of H does not change, the amortized cost of this operation is equal to its O(1) actual cost.

Uniting two Fibonacci heaps

The following procedure unites Fibonacci heaps H₁ and H₂, destroying H₁ and H₂ in the process. It simply concatenates the root lists of H₁ and H₂ and then determines the new minimum node.

FIB-HEAP-UNION(H1, H2)
1  H ← MAKE-FIB-HEAP()
2  min[H] ← min[H1]
3  concatenate the root list of H2 with the root list of H
4  if (min[H1] = NIL) or (min[H2] ≠ NIL and min[H2] < min[H1])
5    then min[H] ← min[H2]
6  n[H] ← n[H1] + n[H2]
7  free the objects H1 and H2
8  return H

Lines 1-3 concatenate the root lists of H₁ and H₂ into a new root list H. Lines 2, 4, and 5 set the minimum node of H , and line 6 sets n[H] to the total number of nodes. The Fibonacci heap objects H₁ and H₂ are freed in line 7, and line 8 returns the resulting Fibonacci heap H. As in the FIB-HEAP-INSERT procedure, no consolidation of trees occurs.

The change in potential is

because t(H) = t(H₁) + t(H₂) and m(H) = m(H₁) + m(H₂). The amortized cost of FIB-HEAP-UNION is therefore equal to its O(1) actual cost.

Extracting the minimum node

The process of extracting the minimum node is the most complicated of the operations presented in this section. It is also where the delayed work of consolidating trees in the root list finally occurs. The following pseudocode extracts the minimum node. The code assumes for convenience that when a node is removed from a linked list, pointers remaining in the list are updated, but pointers in the extracted node are left unchanged. It also uses the auxiliary procedure CONSOLIDATE, which will be presented shortly.

FIB-HEAP-EXTRACT-MIN(H)
 1  z ← min[H]
 2  if z ≠ NIL
 3     then for each child x of z
 4              do add x to the root list of H
 5                 p[x] ← NIL
 6          remove z from the root list of H
 7          if z = right[z]
 8             then min[H] ← NIL
 9             else min[H] ← right[z]
10                  CONSOLIDATE(H)
11          n[H] ← n[H] - 1
12  return z

As shown in Figure 20.3, FIB-HEAP-EXTRACT-MIN works by first making a root out of each of the minimum node's children and removing the minimum node from the root list. It then consolidates the root list by linking roots of equal degree until at most one root remains of each degree.

 
Figure 20.3: The action of FIB-HEAP-EXTRACT-MIN. (a) A Fibonacci heap H. (b) The situation after the minimum node z is removed from the root list and its children are added to the root list. (c)-(e) The array A and the trees after each of the first three iterations of the for loop of lines 3-13 of the procedure CONSOLIDATE. The root list is processed by starting at the node pointed to by min[H ] and following right pointers. Each part shows the values of w and x at the end of an iteration. (f)-(h) The next iteration of the for loop, with the values of w and x shown at the end of each iteration of the while loop of lines 6-12. Part (f) shows the situation after the first time through the while loop. The node with key 23 has been linked to the node with key 7, which is now pointed to by x. In part (g), the node with key 17 has been linked to the node with key 7, which is still pointed to by x. In part (h), the node with key 24 has been linked to the node with key 7. Since no node was previously pointed to by A[3], at the end of the for loop iteration, A[3] is set to point to the root of the resulting tree. (i)-(l) The situation after each of the next four iterations of the for loop. (m) Fibonacci heap H after reconstruction of the root list from the array A and determination of the new min[H] pointer.

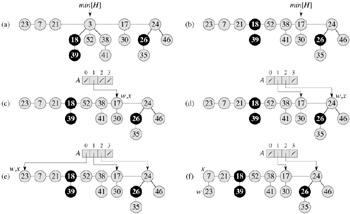
We start in line 1 by saving a pointer z to the minimum node; this pointer is returned at the end. If z = NIL, then Fibonacci heap H is already empty and we are done. Otherwise, as in the BINOMIAL-HEAP-EXTRACT-MIN procedure, we delete node z from H by making all of z's children roots of H in lines 3-5 (putting them into the root list) and removing z from the root list in line 6. If z = right[z] after line 6, then z was the only node on the root list and it had no children, so all that remains is to make the Fibonacci heap empty in line 8 before returning z. Otherwise, we set the pointer min[H] into the root list to point to a node other than z (in this case, right[z]), which is not necessarily going to be the new minimum node when FIB-HEAP-EXTRACT-MIN is done. Figure 20.3(b) shows the Fibonacci heap of Figure 20.3(a) after line 9 has been performed.

The next step, in which we reduce the number of trees in the Fibonacci heap, is consolidating the root list of H; this is performed by the call CONSOLIDATE(H). Consolidating the root list consists of repeatedly executing the following steps until every root in the root list has a distinct degree value.

1. Find two roots x and y in the root list with the same degree, where key[x] ≤ key[y].

2. Link y to x: remove y from the root list, and make y a child of x. This operation is performed by the FIB-HEAP-LINK procedure. The field degree[x] is incremented, and the mark on y, if any, is cleared.

The procedure CONSOLIDATE uses an auxiliary array A[0 ‥ D(n[H])]; if A[i] = y, then y is currently a root with degree[y] = i.

CONSOLIDATE(H)
 1 for i ← 0 to D(n[H])
 2      do A[i] ← NIL
 3 for each node w in the root list of H
 4      do x ← w
 5         d ← degree[x]
 6         while A[d] ≠ NIL
 7             do y ← A[d]      ▹ Another node with the same degree as x.
 8                if key[x] > key[y]
 9                   then exchange x ↔ y
10                FIB-HEAP-LINK(H, y, x)
11                A[d] ← NIL
12                d ← d + 1
13         A[d] ← x
14 min[H] ← NIL
15 for i ← 0 to D(n[H])
16      do if A[i] ≠ NIL
17            then add A[i] to the root list of H
18                 if min[H] = NIL or key[A[i]] < key[min[H]]
19                    then min[H] ← A[i]

FIB-HEAP-LINK(H, y, x)
1  remove y from the root list of H
2  make y a child of x, incrementing degree[x]
3  mark[y] ← FALSE

In detail, the CONSOLIDATE procedure works as follows. Lines 1-2 initialize A by making each entry NIL. The for loop of lines 3-13 processes each root w in the root list. After processing each root w, it ends up in a tree rooted at some node x, which may or may not be identical to w. Of the processed roots, no others will have the same degree as x, and so we will set array entry A[degree[x]] to point to x. When this for loop terminates, at most one root of each degree will remain, and the array A will point to each remaining root.

The while loop of lines 6-12 repeatedly links the root x of the tree containing node w to another tree whose root has the same degree as x, until no other root has the same degree. This while loop maintains the following invariant:

• At the start of each iteration of the while loop, d = degree[x].

We use this loop invariant as follows:

• Initialization: Line 5 ensures that the loop invariant holds the first time we enter the loop.

• Maintenance: In each iteration of the while loop, A[d] points to some root y. Because d = degree[x] = degree[y], we want to link x and y. Whichever of x and y has the smaller key becomes the parent of the other as a result of the link operation, and so lines 8-9 exchange the pointers to x and y if necessary. Next, we link y to x by the call FIB-HEAP-LINK(H, y, x) in line 10. This call increments degree[x] but leaves degree[y] as d. Because node y is no longer a root, the pointer to it in array A is removed in line 11. Because the call of FIB-HEAP-LINK increments the value of degree[x], line 12 restores the invariant that d = degree[x].

• Termination: We repeat the while loop until A[d] = NIL, in which case there is no other root with the same degree as x.

After the while loop terminates, we set A[d] to x in line 13 and perform the next iteration of the for loop.

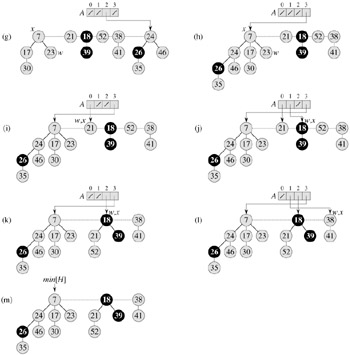
Figures 20.3(c)-(e) show the array A and the resulting trees after the first three iterations of the for loop of lines 3-13. In the next iteration of the for loop, three links occur; their results are shown in Figures 20.3(f)-(h). Figures 20.3(i)-(l) show the result of the next four iterations of the for loop.

All that remains is to clean up. Once the for loop of lines 3-13 completes, line 14 empties the root list, and lines 15-19 reconstruct it from the array A. The resulting Fibonacci heap is shown in Figure 20.3(m). After consolidating the root list, FIB-HEAP-EXTRACT-MIN finishes up by decrementing n[H] in line 11 and returning a pointer to the deleted node z in line 12.

Observe that if all trees in the Fibonacci heap are unordered binomial trees before FIB-HEAP-EXTRACT-MIN is executed, then they are all unordered binomial trees afterward. There are two ways in which trees are changed. First, in lines 3-5 of FIB-HEAP-EXTRACT-MIN, each child x of root z becomes a root. By Exercise 20.2-2, each new tree is itself an unordered binomial tree. Second, trees are linked by FIB-HEAP-LINK only if they have the same degree. Since all trees are unordered binomial trees before the link occurs, two trees whose roots each have k children must have the structure of U_k. The resulting tree therefore has the structure of U_k+1.

We are now ready to show that the amortized cost of extracting the minimum node of an n-node Fibonacci heap is O(D(n)). Let H denote the Fibonacci heap just prior to the FIB-HEAP-EXTRACT-MIN operation.

The actual cost of extracting the minimum node can be accounted for as follows. An O(D(n)) contribution comes from there being at most D(n) children of the minimum node that are processed in FIB-HEAP-EXTRACT-MIN and from the work in lines 1-2 and 14-19 of CONSOLIDATE. It remains to analyze the contribution from the for loop of lines 3-13. The size of the root list upon calling CONSOLIDATE is at most D(n) + t(H) - 1, since it consists of the original t(H) root-list nodes, minus the extracted root node, plus the children of the extracted node, which number at most D(n). Every time through the while loop of lines 6-12, one of the roots is linked to another, and thus the total amount of work performed in the for loop is at most proportional to D(n) + t(H). Thus, the total actual work in extracting the minimum node is O(D(n) + t(H)).

The potential before extracting the minimum node is t(H) + 2m(H), and the potential afterward is at most (D(n) + 1) + 2m(H), since at most D(n) + 1 roots remain and no nodes become marked during the operation. The amortized cost is thus at most

since we can scale up the units of potential to dominate the constant hidden in O(t(H). Intuitively, the cost of performing each link is paid for by the reduction in potential due to the link's reducing the number of roots by one. We shall see in Section 20.4 that D(n) = O(lg n), so that the amortized cost of extracting the minimum node is O(lg n).

Exercises 20.2-1

Show the Fibonacci heap that results from calling FIB-HEAP-EXTRACT-MIN on the Fibonacci heap shown in Figure 20.3(m).

Exercises 20.2-2

Prove that Lemma 19.1 holds for unordered binomial trees, but with property 4′ in place of property 4.

Exercises 20.2-3

Show that if only the mergeable-heap operations are supported, the maximum degree D(n) in an n-node Fibonacci heap is at most ⌊lg n⌋.

Exercises 20.2-4

Professor McGee has devised a new data structure based on Fibonacci heaps. A McGee heap has the same structure as a Fibonacci heap and supports the mergeable-heap operations. The implementations of the operations are the same as for Fibonacci heaps, except that insertion and union perform consolidation as their last step. What are the worst-case running times of operations on McGee heaps? How novel is the professor's data structure?

Exercises 20.2-5

Argue that when the only operations on keys are comparing two keys (as is the case for all the implementations in this chapter), not all of the mergeable-heap operations can run in O(1) amortized time.