| < Day Day Up > |
This section describes two formats, standard form and slack form, that will be useful in specifying and working with linear programs. In standard form, all the constraints are inequalities, whereas in slack form, the constraints are equalities.
In standard form, we are given n real numbers c1, c2, ..., cn; m real numbers b1, b2, ..., bm; and mn real numbers aij for i = 1, 2, ..., m and j = 1, 2, ..., n. We wish to find n real numbers x1, x2, ..., xn that
subject to
Generalizing the terminology we introduced for the two-variable linear program, we call expression (29.16) the objective function and the n + m inequalities in lines (29.17) and (29.18) the constraints. The n constraints in line (29.18) are called the nonnegativity constraints. An arbitrary linear program need not have nonnegativity constraints, but standard form requires them. Sometimes we find it convenient to express a linear program in a more compact form. If we create an m × n matrix A = (aij), an m-dimensional vector b = (bi), an n-dimensional vector c = (cj), and an n-dimensional vector x = (xj), then we can rewrite the linear program defined in (29.16)-(29.18) as
subject to
In line (29.19), cTx is the inner product of two vectors. In line (29.20), Ax is a matrix-vector product, and in line (29.21), x ≥ 0 means that each entry of the vector x must be nonnegative. We see that we can specify a linear program in standard form by a tuple (A, b, c), and we shall adopt the convention that A, b, and c always have the dimensions given above.
We now introduce terminology to describe solutions to linear programs. Some of this terminology was used in the earlier example of a two-variable linear program. We call a setting of the variables ![]() that satisfies all the constraints a feasible solution, whereas a setting of the variables
that satisfies all the constraints a feasible solution, whereas a setting of the variables ![]() that fails to satisfy at least one constraint is called an infeasible solution. We say that a solution
that fails to satisfy at least one constraint is called an infeasible solution. We say that a solution ![]() has objective value
has objective value ![]() . A feasible solution
. A feasible solution ![]() whose objective value is maximum over all feasible solutions is an optimal solution, and we call its objective value
whose objective value is maximum over all feasible solutions is an optimal solution, and we call its objective value ![]() the optimal objective value. If a linear program has no feasible solutions, we say that the linear program is infeasible; otherwise it is feasible. If a linear program has some feasible solutions but does not have a finite optimal objective value, we say that the linear program is unbounded. Exercise 29.1-9 asks you to show that a linear program can have a finite optimal objective value even if the feasible region is not bounded.
the optimal objective value. If a linear program has no feasible solutions, we say that the linear program is infeasible; otherwise it is feasible. If a linear program has some feasible solutions but does not have a finite optimal objective value, we say that the linear program is unbounded. Exercise 29.1-9 asks you to show that a linear program can have a finite optimal objective value even if the feasible region is not bounded.
It is always possible to convert a linear program, given as the minimization or maximization of a linear function subject to linear constraints, into standard form. A linear program may not be in standard form for one of four possible reasons:
The objective function may be a minimization rather than a maximization.
There may be variables without nonnegativity constraints.
There may be equality constraints, which have an equal sign rather than a less-than-or-equal-to sign.
There may be inequality constraints, but instead of having a less-than-or-equal-to sign, they have a greater-than-or-equal-to sign.
When converting one linear program L into another linear program L′, we would like the property that an optimal solution to L′ will yield an optimal solution to L. To capture this idea, we say that two maximization linear programs L and L′ are equivalent if for each feasible solution ![]() to L with objective value z, there is a corresponding feasible solution
to L with objective value z, there is a corresponding feasible solution ![]() to L′ with objective value z, and for each feasible solution
to L′ with objective value z, and for each feasible solution ![]() to L′ with objective value z, there is a corresponding feasible solution
to L′ with objective value z, there is a corresponding feasible solution ![]() to L with objective value z. (This definition does not imply a one-to-one correspondence between feasible solutions.) A minimization linear program L and a maximization linear program L′ are equivalent if for each feasible solution
to L with objective value z. (This definition does not imply a one-to-one correspondence between feasible solutions.) A minimization linear program L and a maximization linear program L′ are equivalent if for each feasible solution ![]() to L′ with objective value z, there is a corresponding feasible solution
to L′ with objective value z, there is a corresponding feasible solution ![]() to L′ with objective value -z, and for each feasible solution
to L′ with objective value -z, and for each feasible solution ![]() to L′ with objective value z, there is a corresponding feasible solution
to L′ with objective value z, there is a corresponding feasible solution ![]() to L with objective value -z.
to L with objective value -z.
We now show how to remove, one by one, each of the possible problems in the list above. After removing each one, we shall argue that the new linear program is equivalent to the old one.
To convert a minimization linear program L into an equivalent maximization linear program L′, we simply negate the coefficients in the objective function. Since L and L′ have identical sets of feasible solutions and, for any feasible solution, the objective value in L is the negative of the objective value in L′, these two linear programs are equivalent. For example, if we have the linear program
|
minimize |
-2x1 |
+ |
3x2 | ||
|
subject to | |||||
|
x1 |
+ |
x2 |
= |
7 |
|
|
x1 |
- |
2x2 |
≤ |
4 |
|
|
x1 |
≥ |
0 , |
and we negate the coefficients of the objective function, we obtain
|
minimize |
2x1 |
- |
3x2 | ||
|
subject to | |||||
|
x1 |
+ |
x2 |
= |
7 |
|
|
x1 |
- |
2x2 |
≤ |
4 |
|
|
x1 |
≥ |
0. |
Next, we show how to convert a linear program in which some of the variables do not have nonnegativity constraints into one in which each variable has a non-negativity constraint. Suppose that some variable xj does not have a nonnegativity constraint. Then we replace each occurrence of xj by ![]() , and add the non-negativity constraints
, and add the non-negativity constraints ![]() and
and ![]() . Thus, if the objective function has a term cjxj , it is replaced by
. Thus, if the objective function has a term cjxj , it is replaced by ![]() , and if constraint i has a term aijxj, it is replaced by
, and if constraint i has a term aijxj, it is replaced by ![]() . Any feasible solution x to the new linear program corresponds to a feasible solution to the original linear program with
. Any feasible solution x to the new linear program corresponds to a feasible solution to the original linear program with ![]() and with the same objective value, and thus the two solutions are equivalent. We apply this conversion scheme to each variable that does not have a nonnegativity constraint to yield an equivalent linear program in which all variables have non-negativity constraints.
and with the same objective value, and thus the two solutions are equivalent. We apply this conversion scheme to each variable that does not have a nonnegativity constraint to yield an equivalent linear program in which all variables have non-negativity constraints.
Continuing the example, we want to ensure that each variable has a corresponding nonnegativity constraint. Variable x1 has such a constraint, but variable x2 does not. Therefore, we replace x2 by two variables ![]() and
and ![]() , and we modify the linear program to obtain
, and we modify the linear program to obtain
subject to
Next, we convert equality constraints into inequality constraints. Suppose that a linear program has an equality constraint f (x1, x2, ..., xn) = b. Since x = y if and only if both x ≥ y and x ≤ y, we can replace this equality constraint by the pair of inequality constraints f (x1, x2, ..., xn) ≤ b and f (x1, x2, ..., xn) ≥ b. Repeating this conversion for each equality constraint yields a linear program in which all constraints are inequalities.
Finally, we can convert the greater-than-or-equal-to constraints to less-than-or-equal-constraints by multiplying these constraints through by -1. That is, any inequality of the form
is equivalent to
Thus, by replacing each coefficient aij by -aij and each value bi by -bi, we obtain an equivalent less-than-or-equal-to constraint.
Finishing our example, we replace the equality in constraint (29.22) by two inequalities, obtaining
subject to
Finally, we negate constraint (29.23). For consistency in variable names, we rename ![]() to x2 and
to x2 and ![]() to x3, obtaining the standard form
to x3, obtaining the standard form
| (29.24) |
subject to
| (29.25) |
| (29.26) |
| (29.27) |
| (29.28) |
To efficiently solve a linear program with the simplex algorithm, we prefer to express it in a form in which some of the constraints are equality constraints. More precisely, we shall convert it into a form in which the nonnegativity constraints are the only inequality constraints, and the remaining constraints are equalities. Let
be an inequality constraint. We introduce a new variable s and rewrite inequality (29.29) as the two constraints
We call s a slack variable because it measures the slack, or difference, between the left-hand and right-hand sides of equation (29.29). Because inequality (29.29) is true if and only if both equation (29.30) and inequality (29.31) are true, we can apply this conversion to each inequality constraint of a linear program, obtaining an equivalent linear program in which the only inequality constraints are the nonnegativity constraints. When converting from standard to slack form, we shall use xn+i (instead of s) to denote the slack variable associated with the ith inequality. The ith constraint is therefore
| (29.32) |
along with the nonnegativity constraint xn+i ≥ 0.
Applying this conversion to each constraint of a linear program in standard form, we obtain a linear program in a different form. For example, for the linear program described in (29.24)-(29.28), we introduce slack variables x4, x5, and x6, obtaining maximize
| (29.33) |
subject to
| (29.34) |
| (29.35) |
| (29.36) |
| (29.37) |
In this linear program, all the constraints except for the nonnegativity constraints are equalities, and each variable is subject to a nonnegativity constraint. We write each equality constraint with one of the variables on the left-hand side of the equality and all others on the right-hand side. Furthermore, each equation has the same set of variables on the right-hand side, and these variables are also the only ones that appear in the objective function. The variables on the left-hand side of the equalities are called basic variables, and those on the right-hand side are called nonbasic variables.
For linear programs that satisfy these conditions, we shall sometimes omit the words "maximize" and "subject to," and we shall omit the explicit nonnegativity constraints. We shall also use the variable z to denote the value of the objective function. We call the resulting format slack form. If we write the linear program given in (29.33)-(29.37) in slack form, we obtain
| (29.38) |
| (29.39) |
| (29.40) |
| (29.41) |
As with standard form, it will be convenient to have a more concise notation for describing a slack form. As we shall see in Section 29.3, the sets of basic and nonbasic variables will change as the simplex algorithm runs. We use N to denote the set of indices of the nonbasic variables and B to denote the set of indices of the basic variables. We will always have that |N| = n, |B| = m, and N ∪ B = {1, 2, ..., n + m}. The equations will be indexed by the entries of B, and the variables on the right-hand sides will be indexed by the entries of N. As in standard form, we use bi , cj , and aij to denote constant terms and coefficients. We also use v to denote an optional constant term in the objective function. Thus we can concisely define a slack form by a tuple (N, B, A, b, c, v), denoting the slack form
| (29.42) |
in which all variables x are constrained to be nonnegative. Because we subtract the sum ![]() in (29.43), the values aij are actually the negatives of the coefficients as they "appear" in the slack form.
in (29.43), the values aij are actually the negatives of the coefficients as they "appear" in the slack form.
For example, in the slack form
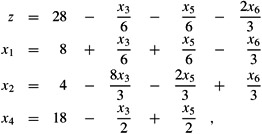
we have B = {1, 2, 4}, N = {3, 5, 6},

c = c3 c5 c6)T = (-1/6 -1/6 -2/3)T, and v = 28. Note that the indices into A, b, and c are not necessarily sets of contiguous integers; they depend on the index sets B and N. As an example of the entries of A being the negatives of the coefficients as they appear in the slack form, observe that the equation for x1 includes the term x3/6, yet the coefficient a13 is actually -1/6 rather than +1/6.
If we express the linear program in (29.24)-(29.28) in the compact notation of (29.19)-(29.21), what are n, m, A, b, and c?
Give three feasible solutions to the linear program in (29.24)-(29.28). What is the objective value of each one?
Convert the following linear program into standard form:
|
minimize |
2x1 |
+ |
7x2 | |||
|
subject to | ||||||
|
x1 |
= |
7 |
||||
|
3x1 |
+ |
x2 |
≥ |
24 |
||
|
x2 |
≥ |
0 |
||||
|
x3 |
≤ |
0 . |
Convert the following linear program into slack form:
|
maximize |
2x1 |
- |
6x3 | ||||
|
subject to | |||||||
|
x1 |
+ |
+x2 |
- |
x3 |
≤ |
7 |
|
|
3x1 |
- |
x2 |
≥ |
8 |
|||
|
-x1 |
+ |
2x2 |
+ |
2x3 |
≥ |
0 |
|
|
x1, x2, x3 |
≥ |
0 . |
|||||
What are the basic and nonbasic variables?
Show that the following linear program is infeasible:
|
maximize |
3x1 |
- |
2x2 | ||
|
subject to | |||||
|
x1 |
+ |
x2 |
≤ |
2 |
|
|
-2x1 |
- |
2x2 |
≤ |
-10 |
|
|
x1, x2 |
≥ |
0 . |
|||
Show that the following linear program is unbounded:
|
maximize |
x1 |
- |
x2 | ||
|
subject to | |||||
|
-2x1 |
+ |
x2 |
≤ |
-1 |
|
|
-x1 |
- |
2x2 |
≤ |
-2 |
|
|
x1, x2 |
≥ |
0 . |
|||
| < Day Day Up > |