Step 1: The structure of an optimal binary search tree

To characterize the optimal substructure of optimal binary search trees, we start with an observation about subtrees. Consider any subtree of a binary search tree. It must contain keys in a contiguous range k_i, ..., k_j, for some 1 ≤ i ≤ j ≤ n. In addition, a subtree that contains keys k_i, ..., k_j must also have as its leaves the dummy keys d_i-1, ..., d_j.

Now we can state the optimal substructure: if an optimal binary search tree T has a subtree T′ containing keys k_i, ..., k_j, then this subtree T′ must be optimal as well for the subproblem with keys k_i, ..., k_j and dummy keys d_i-1, ..., d_j. The usual cut-and-paste argument applies. If there were a subtree T" whose expected cost is lower than that of T′, then we could cut T′ out of T and paste in T", resulting in a binary search tree of lower expected cost than T, thus contradicting the optimality of T.

We need to use the optimal substructure to show that we can construct an optimal solution to the problem from optimal solutions to subproblems. Given keys k_i, ..., k_j, one of these keys, say k_r (i ≤ r ≤ j), will be the root of an optimal subtree containing these keys. The left subtree of the root k_r will contain the keys k_i, ..., k_r-1 (and dummy keys d_i-1, ..., d_r-1), and the right subtree will contain the keys k_r+1, ..., k_j (and dummy keys d_r, ..., d_j). As long as we examine all candidate roots k_r, where i ≤ r ≤ j, and we determine all optimal binary search trees containing k_i, ..., k_r-1 and those containing k_r+1, ..., k_j, we are guaranteed that we will find an optimal binary search tree.

There is one detail worth noting about "empty" subtrees. Suppose that in a subtree with keys k_i, ..., k_j, we select k_i as the root. By the above argument, k_i's left subtree contains the keys k_i, ..., k_i-1. It is natural to interpret this sequence as containing no keys. Bear in mind, however, that subtrees also contain dummy keys. We adopt the convention that a subtree containing keys k_i, ..., k_i-1 has no actual keys but does contain the single dummy key d_i-1. Symmetrically, if we select k_j as the root, then k_j's right subtree contains the keys k_{j +1}, ..., k_j; this right subtree contains no actual keys, but it does contain the dummy key d_j.

Step 2: A recursive solution

We are ready to define the value of an optimal solution recursively. We pick our subproblem domain as finding an optimal binary search tree containing the keys k_i, ..., k_j, where i ≥ 1, j ≤ n, and j ≥ i - 1. (It is when j = i - 1 that there are no actual keys; we have just the dummy key d_i-1.) Let us define e[i, j] as the expected cost of searching an optimal binary search tree containing the keys k_i, ..., k_j. Ultimately, we wish to compute e[1, n].

The easy case occurs when j = i - 1. Then we have just the dummy key d_i-1. The expected search cost is e[i, i - 1] = q_i-1.

When j ≥ i, we need to select a root k_r from among k_i, ..., k_j and then make an optimal binary search tree with keys k_i, ..., k_r-1 its left subtree and an optimal binary search tree with keys k_r+1, ..., k_j its right subtree. What happens to the expected search cost of a subtree when it becomes a subtree of a node? The depth of each node in the subtree increases by 1. By equation (15.16), the expected search cost of this subtree increases by the sum of all the probabilities in the subtree. For a subtree with keys k_i, ..., k_j, let us denote this sum of probabilities as

(15.17)

Thus, if k_r is the root of an optimal subtree containing keys k_i, ..., k_j, we have

e[i, j ] = p_r + (e[i, r - 1] + w(i, r - 1)) + (e[r + 1, j] + w(r + 1, j)).

Noting that

w(i, j) = w(i, r - 1) + p_r + w(r + 1, j),

we rewrite e[i, j] as

(15.18)

The recursive equation (15.18) assumes that we know which node k_r to use as the root. We choose the root that gives the lowest expected search cost, giving us our final recursive formulation:

(15.19)

The e[i, j] values give the expected search costs in optimal binary search trees. To help us keep track of the structure of optimal binary search trees, we define root[i, j], for 1 ≤ i ≤ j ≤ n, to be the index r for which k_r is the root of an optimal binary search tree containing keys k_i, ..., k_j. Although we will see how to compute the values of root[i, j], we leave the construction of the optimal binary search tree from these values as Exercise 15.5-1.

Step 3: Computing the expected search cost of an optimal binary search tree

At this point, you may have noticed some similarities between our characterizations of optimal binary search trees and matrix-chain multiplication. For both problem domains, our subproblems consist of contiguous index subranges. A direct, recursive implementation of equation (15.19) would be as inefficient as a direct, recursive matrix-chain multiplication algorithm. Instead, we store the e[i, j] values in a table e[1 ‥ n + 1, 0 ‥ n]. The first index needs to run to n + 1 rather than n because in order to have a subtree containing only the dummy key d_n, we will need to compute and store e[n + 1, n]. The second index needs to start from 0 because in order to have a subtree containing only the dummy key d₀, we will need to compute and store e[1, 0]. We will use only the entries e[i, j] for which j ≥ i - 1. We also use a table root[i, j], for recording the root of the subtree containing keys k_i, ..., k_j. This table uses only the entries for which 1 ≤ i ≤ j ≤ n.

We will need one other table for efficiency. Rather than compute the value of w(i, j) from scratch every time we are computing e[i, j]-which would take Θ(j - i) additions-we store these values in a table w[1 ‥ n + 1, 0 ‥ n]. For the base case, we compute w[i, i - 1] = q_i-1 for 1 ≤ i ≤ n. For j ≥ i, we compute

(15.20)

Thus, we can compute the Θ(n²) values of w[i, j] in Θ(1) time each.

The pseudocode that follows takes as inputs the probabilities p₁, ..., p_n and q₀, ..., q_n and the size n, and it returns the tables e and root.

OPTIMAL-BST(p, q, n)
 1  for i ← 1 to n + 1
 2       do e[i, i - 1] ← qi-1
 3          w[i, i - 1] ← qi-1
 4  for l ← 1 to n
 5       do for i ← 1 to n - l + 1
 6               do j ← i + l - 1
 7                  e[i, j] ← ∞
 8                  w[i, j] ← w[i, j - 1] + pj + qj
 9                  for r ← i to j
10                       do t ← e[i, r - 1] + e[r + 1, j] + w[i, j]
11                          if t < e[i, j]
12                             then e[i, j] ← t
13                                  root[i, j] ← r
14  return e and root

From the description above and the similarity to the MATRIX-CHAIN-ORDER procedure in Section 15.2, the operation of this procedure should be fairly straightforward. The for loop of lines 1-3 initializes the values of e[i, i - 1] and w[i, i - 1]. The for loop of lines 4-13 then uses the recurrences (15.19) and (15.20) to compute e[i, j] and w[i, j] for all 1 ≤ i ≤ j ≤ n. In the first iteration, when l = 1, the loop computes e[i, i] and w[i, i] for i = 1, 2, ..., n. The second iteration, with l = 2, computes e[i, i + 1] and w[i, i +1] for i = 1, 2, ..., n - 1, and so forth. The innermost for loop, in lines 9-13, tries each candidate index r to determine which key k_r to use as the root of an optimal binary search tree containing keys k_i, ..., k_j. This for loop saves the current value of the index r in root[i, j] whenever it finds a better key to use as the root.

Figure 15.8 shows the tables e[i, j], w[i, j], and root[i, j] computed by the procedure OPTIMAL-BST on the key distribution shown in Figure 15.7. As in the matrix-chain multiplication example, the tables are rotated to make the diagonals run horizontally. OPTIMAL-BST computes the rows from bottom to top and from left to right within each row.

Figure 15.8: The tables e[i, j], w[i, j], and root[i, j] computed by OPTIMAL-BST on the key distribution shown in Figure 15.7. The tables are rotated so that the diagonals run horizontally.

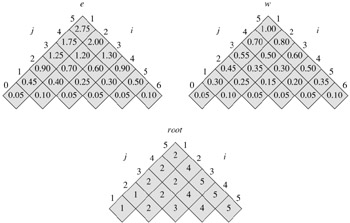
The OPTIMAL-BST procedure takes Θ(n³) time, just like MATRIX-CHAIN-ORDER. It is easy to see that the running time is O(n³), since its for loops are nested three deep and each loop index takes on at most n values. The loop indices in OPTIMAL-BST do not have exactly the same bounds as those in MATRIX-CHAIN-ORDER, but they are within at most 1 in all directions. Thus, like MATRIX-CHAIN-ORDER, the OPTIMAL-BST procedure takes Ω(n³) time.

Exercises 15.5-1

Write pseudocode for the procedure CONSTRUCT-OPTIMAL-BST(root) which, given the table root, outputs the structure of an optimal binary search tree. For the example in Figure 15.8, your procedure should print out the structure

• k₂ is the root

• k₁ is the left child of k₂

• d₀ is the left child of k₁

• d₁ is the right child of k₁

• k₅ is the right child of k₂

• k₄ is the left child of k₅

• k₃ is the left child of k₄

• d₂ is the left child of k₃

• d₃ is the right child of k₃

• d₄ is the right child of k₄

• d₅ is the right child of k₅

corresponding to the optimal binary search tree shown in Figure 15.7(b).

Exercises 15.5-2

Determine the cost and structure of an optimal binary search tree for a set of n = 7 keys with the following probabilities:

i	0	1	2	3	4	5	6	7
pi		0.04	0.06	0.08	0.02	0.10	0.12	0.14
qi	0.06	0.06	0.06	0.06	0.05	0.05	0.05	0.05

Exercises 15.5-3

Suppose that instead of maintaining the table w[i, j], we computed the value of w(i, j) directly from equation (15.17) in line 8 of OPTIMAL-BST and used this computed value in line 10. How would this change affect the asymptotic running time of OPTIMAL-BST?

Exercises 15.5-4: ⋆

Knuth [184] has shown that there are always roots of optimal subtrees such that root[i, j - 1] ≤ root[i, j] ≤ root[i + 1, j] for all 1 ≤ i < j ≤ n. Use this fact to modify the OPTIMAL-BST procedure to run in Θ(n²) time.

Problems 15-1: Bitonic euclidean traveling-salesman problem

The euclidean traveling-salesman problem is the problem of determining the shortest closed tour that connects a given set of n points in the plane. Figure 15.9(a) shows the solution to a 7-point problem. The general problem is NP-complete, and its solution is therefore believed to require more than polynomial time (see Chapter 34).

Figure 15.9: Seven points in the plane, shown on a unit grid. (a) The shortest closed tour, with length approximately 24.89. This tour is not bitonic. (b) The shortest bitonic tour for the same set of points. Its length is approximately 25.58.

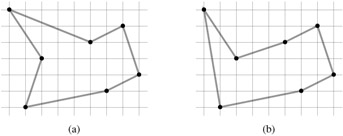
J. L. Bentley has suggested that we simplify the problem by restricting our attention to bitonic tours, that is, tours that start at the leftmost point, go strictly left to right to the rightmost point, and then go strictly right to left back to the starting point. Figure 15.9(b) shows the shortest bitonic tour of the same 7 points. In this case, a polynomial-time algorithm is possible.

Describe an O(n²)-time algorithm for determining an optimal bitonic tour. You may assume that no two points have the same x-coordinate. (Hint: Scan left to right, maintaining optimal possibilities for the two parts of the tour.)

Problems 15-2: Printing neatly

Consider the problem of neatly printing a paragraph on a printer. The input text is a sequence of n words of lengths l₁, l₂, ..., l_n, measured in characters. We want to print this paragraph neatly on a number of lines that hold a maximum of M characters each. Our criterion of "neatness" is as follows. If a given line contains words i through j, where i ≤ j, and we leave exactly one space between words, the number of extra space characters at the end of the line is , which must be nonnegative so that the words fit on the line. We wish to minimize the sum, over all lines except the last, of the cubes of the numbers of extra space characters at the ends of lines. Give a dynamic-programming algorithm to print a paragraph of n words neatly on a printer. Analyze the running time and space requirements of your algorithm.

Problems 15-3: Edit distance

In order to transform one source string of text x[1 ‥ m] to a target string y[1 ‥ n], we can perform various transformation operations. Our goal is, given x and y, to produce a series of transformations that change x to y. We use an array z-assumed to be large enough to hold all the characters it will need-to hold the intermediate results. Initially, z is empty, and at termination, we should have z[j] = y[j] for j = 1, 2, ..., n. We maintain current indices i into x and j into z, and the operations are allowed to alter z and these indices. Initially, i = j = 1. We are required to examine every character in x during the transformation, which means that at the end of the sequence of transformation operations, we must have i = m + 1.

There are six transformation operations:

• Copy a character from x to z by setting z[j] ← x[i] and then incrementing both i and j. This operation examines x[i].

• Replace a character from x by another character c, by setting z[j] ← c, and then incrementing both i and j. This operation examines x[i].

• Delete a character from x by incrementing i but leaving j alone. This operation examines x[i].

• Insert the character c into z by setting z[j] ← c and then incrementing j, but leaving i alone. This operation examines no characters of x.

• Twiddle (i.e., exchange) the next two characters by copying them from x to z but in the opposite order; we do so by setting z[j] ← x[i + 1] and z[j + 1] ← x[i] and then setting i ← i + 2 and j ← j + 2. This operation examines x[i] and x[i + 1].

• Kill the remainder of x by setting i ← m + 1. This operation examines all characters in x that have not yet been examined. If this operation is performed, it must be the final operation.

As an example, one way to transform the source string algorithm to the target string altruistic is to use the following sequence of operations, where the underlined characters are x[i] and z[j] after the operation:

Note that there are several other sequences of transformation operations that transform algorithm to altruistic.

Each of the transformation operations has an associated cost. The cost of an operation depends on the specific application, but we assume that each operation's cost is a constant that is known to us. We also assume that the individual costs of the copy and replace operations are less than the combined costs of the delete and insert operations; otherwise, the copy and replace operations would not be used. The cost of a given sequence of transformation operations is the sum of the costs of the individual operations in the sequence. For the sequence above, the cost of transforming algorithm to altruistic is

(3 · cost(copy)) + cost(replace) + cost(delete) + (4 · cost(insert)) + cost(twiddle) + cost(kill).

1. Given two sequences x[1 ‥ m] and y[1 ‥ n] and set of transformation-operation costs, the edit distance from x to y is the cost of the least expensive operation sequence that transforms x to y. Describe a dynamic-programming algorithm that finds the edit distance from x[1 ‥ m] to y[1 ‥ n] and prints an optimal operation sequence. Analyze the running time and space requirements of your algorithm.

The edit-distance problem is a generalization of the problem of aligning two DNA sequences (see, for example, Setubal and Meidanis [272, Section 3.2]). There are several methods for measuring the similarity of two DNA sequences by aligning them. One such method to align two sequences x and y consists of inserting spaces at arbitrary locations in the two sequences (including at either end) so that the resulting sequences x′ and y′ have the same length but do not have a space in the same position (i.e., for no position j are both x′[j] and y′[j] a space.) Then we assign a "score" to each position. Position j receives a score as follows:

• +1 if x′[j] = y′[j] and neither is a space,

• -1 if x′[j] ≠ y′[j] and neither is a space,

• -2 if either x′[j] or y′[j] is a space.

The score for the alignment is the sum of the scores of the individual positions. For example, given the sequences x = GATCGGCAT and y = CAATGTGAATC, one alignment is

G ATCG GCAT
CAAT GTGAATC
-*++*+*+-++*

A + under a position indicates a score of +1 for that position, a - indicates a score of -1, and a ⋆ indicates a score of -2, so that this alignment has a total score of 6 · 1 - 2 · 1 - 4 · 2 _ -4.

2. Explain how to cast the problem of finding an optimal alignment as an edit distance problem using a subset of the transformation operations copy, replace, delete, insert, twiddle, and kill.

Problems 15-4: Planning a company party

Professor Stewart is consulting for the president of a corporation that is planning a company party. The company has a hierarchical structure; that is, the supervisor relation forms a tree rooted at the president. The personnel office has ranked each employee with a conviviality rating, which is a real number. In order to make the party fun for all attendees, the president does not want both an employee and his or her immediate supervisor to attend.

Professor Stewart is given the tree that describes the structure of the corporation, using the left-child, right-sibling representation described in Section 10.4. Each node of the tree holds, in addition to the pointers, the name of an employee and that employee's conviviality ranking. Describe an algorithm to make up a guest list that maximizes the sum of the conviviality ratings of the guests. Analyze the running time of your algorithm.

Problems 15-5: Viterbi algorithm

We can use dynamic programming on a directed graph G = (V, E) for speech recognition. Each edge (u, v) ∈ E is labeled with a sound σ(u, v) from a finite set Σ of sounds. The labeled graph is a formal model of a person speaking a restricted language. Each path in the graph starting from a distinguished vertex v₀ ∈ V corresponds to a possible sequence of sounds produced by the model. The label of a directed path is defined to be the concatenation of the labels of the edges on that path.

1. Describe an efficient algorithm that, given an edge-labeled graph G with distinguished vertex v₀ and a sequence s = 〈σ₁, σ₂, ..., σ_k〉 of characters from Σ, returns a path in G that begins at v₀ and has s as its label, if any such path exists. Otherwise, the algorithm should return NO-SUCH-PATH. Analyze the running time of your algorithm. (Hint: You may find concepts from Chapter 22 useful.)

Now, suppose that every edge (u, v) ∈ E has also been given an associated nonnegative probability p(u, v) of traversing the edge (u, v) from vertex u and thus producing the corresponding sound. The sum of the probabilities of the edges leaving any vertex equals 1. The probability of a path is defined to be the product of the probabilities of its edges. We can view the probability of a path beginning at v₀ as the probability that a "random walk" beginning at v₀ will follow the specified path, where the choice of which edge to take at a vertex u is made probabilistically according to the probabilities of the available edges leaving u.

2. Extend your answer to part (a) so that if a path is returned, it is a most probable path starting at v₀ and having label s. Analyze the running time of your algorithm.

Problems 15-6: Moving on a checkerboard

Suppose that you are given an n × n checkerboard and a checker. You must move the checker from the bottom edge of the board to the top edge of the board according to the following rule. At each step you may move the checker to one of three squares:

1. the square immediately above,

2. the square that is one up and one to the left (but only if the checker is not already in the leftmost column),

3. the square that is one up and one to the right (but only if the checker is not already in the rightmost column).

Each time you move from square x to square y, you receive p(x, y) dollars. You are given p(x, y) for all pairs (x, y) for which a move from x to y is legal. Do not assume that p(x, y) is positive.

Give an algorithm that figures out the set of moves that will move the checker from somewhere along the bottom edge to somewhere along the top edge while gathering as many dollars as possible. Your algorithm is free to pick any square along the bottom edge as a starting point and any square along the top edge as a destination in order to maximize the number of dollars gathered along the way. What is the running time of your algorithm?

Problems 15-7: Scheduling to maximize profit

Suppose you have one machine and a set of n jobs a₁, a₂, ..., a_n to process on that machine. Each job a_j has a processing time t_j, a profit p_j, and a deadline d_j. The machine can process only one job at a time, and job a_j must run uninterruptedly for t_j consecutive time units. If job a_j is completed by its deadline d_j, you receive a profit p_j, but if it is completed after its deadline, you receive a profit of 0. Give an algorithm to find the schedule that obtains the maximum amount of profit, assuming that all processing times are integers between 1 and n. What is the running time of your algorithm?