Finite automata

A finite automaton M is a 5-tuple (Q, q₀, A, Σ, δ), where

• Q is a finite set of states,

• q₀ ∈ Q is the start state,

• A ⊆ Q is a distinguished set of accepting states,

• Σ is a finite input alphabet,

• δ is a function from Q × Σ into Q, called the transition function of M.

The finite automaton begins in state q₀ and reads the characters of its input string one at a time. If the automaton is in state q and reads input character a, it moves ("makes a transition") from state q to state δ(q, a). Whenever its current state q is a member of A, the machine M is said to have accepted the string read so far. An input that is not accepted is said to be rejected. Figure 32.6 illustrates these definitions with a simple two-state automaton.

Figure 32.6: A simple two-state finite automaton with state set Q = {0, 1}, start state q₀ = 0, and input alphabet Σ = {a, b}. (a) A tabular representation of the transition function δ. (b) An equivalent state-transition diagram. State 1 is the only accepting state (shown blackened). Directed edges represent transitions. For example, the edge from state 1 to state 0 labeled b indicates δ(1, b) = 0. This automaton accepts those strings that end in an odd number of a's. More precisely, a string x is accepted if and only if x = yz, where y = ε or y ends with a b, and z = a^k, where k is odd. For example, the sequence of states this automaton enters for input abaaa (including the start state) is 〈0, 1, 0, 1, 0, 1〉, and so it accepts this input. For input abbaa, the sequence of states is 〈0, 1, 0, 0, 1, 0〉, and so it rejects this input.

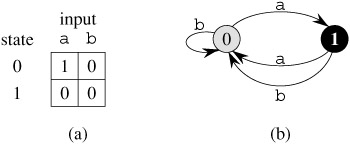
A finite automaton M induces a function φ, called the final-state function, from Σ* to Q such that φ(w) is the state M ends up in after scanning the string w. Thus, M accepts a string w if and only if φ(w) ∈ A. The function φ is defined by the recursive relation

String-matching automata

There is a string-matching automaton for every pattern P; this automaton must be constructed from the pattern in a preprocessing step before it can be used to search the text string. Figure 32.7 illustrates this construction for the pattern P = ababaca. From now on, we shall assume that P is a given fixed patternstring; for brevity, we shall not indicate the dependence upon P in our notation.

Figure 32.7: (a) A state-transition diagram for the string-matching automaton that accepts all strings ending in the string ababaca. State 0 is the start state, and state 7 (shown blackened) is the only accepting state. A directed edge from state i to state j labeled a represents δ(i, a) = j. The right-going edges forming the "spine" of the automaton, shown heavy in the figure, correspond to successful matches between pattern and input characters. The left-going edges correspond to failing matches. Some edges corresponding to failing matches are not shown; by convention, if a state i has no outgoing edge labeled a for some a ∈ Σ, then δ(i, a) = 0. (b) The corresponding transition function δ, and the pattern string P = ababaca. The entries corresponding to successful matches between pattern and input characters are shown shaded. (c) The operation of the automaton on the text T = abababacaba. Under each text character T [i] is given the state φ(T_i) the automaton is in after processing the prefix T_i. One occurrence of the pattern is found, ending in position 9.

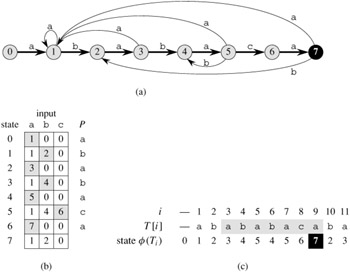
In order to specify the string-matching automaton corresponding to a given pattern P[1 ‥ m], we first define an auxiliary function σ , called the suffix function corresponding to P. The function σ is a mapping from Σ* to {0, 1, . . . , m} such that σ(x) is the length of the longest prefix of P that is a suffix of x:

σ(x) = max {k : P_k ⊐ x}.

The suffix function σ is well defined since the empty string P₀ = ε is a suffix of every string. As examples, for the pattern P = ab, we have σ(ε) = 0, σ(ccaca) = 1, and σ(ccab) = 2. For a pattern P of length m, we have σ(x) = m if and only if P ⊐ x. It follows from the definition of the suffix function that if x ⊐ y, then σ(x) ≤ σ(y).

We define the string-matching automaton that corresponds to a given pattern P[1 ‥ m] as follows.

• The state set Q is {0, 1, . . . , m}. The start state q₀ is state 0, and state m is the only accepting state.

• The transition function δ is defined by the following equation, for any state q and character a:

  (32.3)

Here is an intuitive rationale for defining δ(q, a) = σ(P_qa). The machine maintains as an invariant of its operation that

(32.4)

this result is proved as Theorem 32.4 below. In words, this means that after scanning the first i characters of the text string T , the machine is in state φ(T_i) = q, where q = σ(T_i) is the length of the longest suffix of T_i that is also a prefix of the pattern P. If the next character scanned is T [i + 1] = a, then the machine should make a transition to state σ(T_i+1) = σ(T_ia). The proof of the theorem shows that σ(T_ia) = σ(P_qa). That is, to compute the length of the longest suffix of T_ia that is a prefix of P, we can compute the longest suffix of P_qa that is a prefix of P. At each state, the machine only needs to know the length of the longest prefix of P that is a suffix of what has been read so far. Therefore, setting δ(q, a) = σ(P_qa) maintains the desired invariant (32.4). This informal argument will be made rigorous shortly.

In the string-matching automaton of Figure 32.7, for example, δ(5, b) = 4. We make this transition because if the automaton reads a b in state q = 5, then P_q b = ababab, and the longest prefix of P that is also a suffix of ababab is P₄ = abab.

To clarify the operation of a string-matching automaton, we now give a simple, efficient program for simulating the behavior of such an automaton (represented by its transition function δ) in finding occurrences of a pattern P of length m in an input text T [1 ‥ n]. As for any string-matching automaton for a pattern of length m, the state set Q is {0, 1, . . . , m}, the start state is 0, and the only accepting state is state m.

FINITE-AUTOMATON-MATCHER(T, δ, m)
1  n ← length[T]
2  q ← 0
3  for i ← 1 to n
4      do q ← δ(q, T[i])
5         if q = m
6            then print "Pattern occurs with shift" i - m

The simple loop structure of FINITE-AUTOMATON-MATCHER implies that its matching time on a text string of length n is Θ(n). This matching time, however, does not include the preprocessing time required to compute the transition function δ. We address this problem later, after proving that the procedure FINITE-AUTOMATON-MATCHER operates correctly.

Consider the operation of the automaton on an input text T [1 ‥ n]. We shall prove that the automaton is in state σ(T_i) after scanning character T [i]. Since σ(T_i) = m if and only if P ⊐ T_i, the machine is in the accepting state m if and only if the pattern P has just been scanned. To prove this result, we make use of the following two lemmas about the suffix function σ.

Lemma 32.2: (Suffix-function inequality)

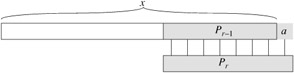
For any string x and character a, we have σ(xa) ≤ σ(x) + 1.

Proof Referring to Figure 32.8, let r = σ(xa). If r = 0, then the conclusion σ(xa) = r ≤ σ(x) + 1 is trivially satisfied, by the nonnegativity of σ(x). So assume that r > 0. Now, P_r ⊐ xa, by the definition of σ. Thus, P_r-1 ⊐ x, by dropping the a from the end of P_r and from the end of xa. Therefore, r -1 ≤ σ(x), since σ(x) is largest k such that P_k ⊐ x, and σ(xa) = r ≤ σ(x) + 1.

Figure 32.8: An illustration for the proof of Lemma 32.2. The figure shows that r ≤ σ(x) + 1, where r = σ(xa).

Lemma 32.3: (Suffix-function recursion lemma)

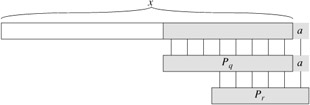
For any string x and character a, if q = σ(x), then σ(xa) = σ(P_qa).

Proof From the definition of σ, we have P_q ⊐ x. As Figure 32.9 shows, we also have P_qa ⊐ xa. If we let r = σ (xa), then r ≤ q + 1 by Lemma 32.2. Since P_qa ⊐ xa, P_r ⊐ xa, and |P_r| ≤ |P_qa|, Lemma 32.1 implies that P_r ⊐ P_qa. Therefore, r ≤ σ(P_qa), that is, σ(xa) ≤ σ(P_qa). But we also have σ(P_qa) ≤ σ(xa), since P_qa ⊐ xa. Thus, σ(xa) = σ(P_qa).

Figure 32.9: An illustration for the proof of Lemma 32.3. The figure shows that r = σ(P_qa), where q = σ(x) and r = σ(xa).

We are now ready to prove our main theorem characterizing the behavior of a string-matching automaton on a given input text. As noted above, this theorem shows that the automaton is merely keeping track, at each step, of the longest prefix of the pattern that is a suffix of what has been read so far. In other words, the automaton maintains the invariant (32.4).

Theorem 32.4

If φ is the final-state function of a string-matching automaton for a given pattern P and T[1 ‥ n] is an input text for the automaton, then

φ(T_i) = σ(T_i)

for i = 0, 1, . . . , n.

Proof The proof is by induction on i. For i = 0, the theorem is trivially true, since T₀ = ε. Thus, φ(T₀) = 0 = σ(T₀).

Now, we assume that φ(T_i) = σ(T_i) and prove that φ(T_i+1) = σ(T_i+1). Let q denote φ(T_i), and let a denote T[i + 1]. Then,

φ(Ti+1)	=	φ(Tia)	(by the definitions of Ti+1 and a)
	=	δ(φ(Ti), a)	(by the definition of φ)
	=	δ(q, a)	(by the definition of q)
	=	σ(Pqa)	(by the definition (32.3) of δ)
	=	σ(Tia)	(by Lemma 32.3 and induction)
	=	σ(Ti+1)	(by the definition of Ti+1).

By Theorem 32.4, if the machine enters state q on line 4, then q is the largest value such that P_q ⊐ T_i. Thus, we have q = m on line 5 if and only if an occurrence of the pattern P has just been scanned. We conclude that FINITE-AUTOMATON-MATCHER operates correctly.

Computing the transition function

The following procedure computes the transition function δ from a given pattern P[1 ‥ m].

COMPUTE-TRANSITION-FUNCTION(P, Σ)
1 m ← length[P]
2 for q ← 0 to m
3     do for each character a ∈ Σ
4            do k ← min(m + 1, q + 2)
5               repeat k ← k - 1
6                 until Pk ⊐ Pqa
7               δ(q, a) ← k
8 return δ

This procedure computes δ(q, a) in a straightforward manner according to its definition. The nested loops beginning on lines 2 and 3 consider all states q and characters a, and lines 4-7 set δ(q, a) to be the largest k such that P_k ⊐ P_qa. The code starts with the largest conceivable value of k, which is min(m, q + 1), and decreases k until P_k ⊐ P_qa.

The running time of COMPUTE-TRANSITION-FUNCTION is O(m³ |Σ|), because the outer loops contribute a factor of m |Σ|, the inner repeat loop can run at most m + 1 times, and the test P_k ⊐ P_qa on line 6 can require comparing up to m characters. Much faster procedures exist; the time required to compute δ from P can be improved to O(m |Σ|) by utilizing some cleverly computed information about the pattern P (see Exercise 32.4-6). With this improved procedure for computing δ, we can find all occurrences of a length-m pattern in a length-n text over an alphabet Σ with O(m |Σ|) preprocessing time and Θ(n) matching time.

Exercises 32.3-1

Construct the string-matching automaton for the pattern P = aabab and illustrate its operation on the text string T = aaababaabaababaab.

Exercises 32.3-2

Draw a state-transition diagram for a string-matching automaton for the pattern ababbabbababbababbabb over the alphabet Σ = {a, b}.

Exercises 32.3-3

We call a pattern P nonoverlappable if P_k ⊐ P_q implies k = 0 or k = q. Describe the state-transition diagram of the string-matching automaton for a nonoverlappable pattern.

Exercises 32.3-4: ★

Given two patterns P and P′, describe how to construct a finite automaton that determines all occurrences of either pattern. Try to minimize the number of states in your automaton.

Exercises 32.3-5

Given a pattern P containing gap characters (see Exercise 32.1-4), show how to build a finite automaton that can find an occurrence of P in a text T in O(n) matching time, where n = |T|.