32.2 The Rabin-Karp algorithm

Rabin and Karp have proposed a string-matching algorithm that performs well in practice and that also generalizes to other algorithms for related problems, such as two-dimensional pattern matching. The Rabin-Karp algorithm uses Θ(m) preprocessing time, and its worst-case running time is Θ((n - m +1)m). Based on certain assumptions, however, its average-case running time is better.

This algorithm makes use of elementary number-theoretic notions such as the equivalence of two numbers modulo a third number. You may want to refer to Section 31.1 for the relevant definitions.

For expository purposes, let us assume that Σ = {0, 1, 2, . . . , 9}, so that each character is a decimal digit. (In the general case, we can assume that each character is a digit in radix-d notation, where d = |Σ|.) We can then view a string of k consecutive characters as representing a length-k decimal number. The character string 31415 thus corresponds to the decimal number 31,415. Given the dual interpretation of the input characters as both graphical symbols and digits, we find it convenient in this section to denote them as we would digits, in our standard text font.

Given a pattern P[1 ‥ m], we let p denote its corresponding decimal value. In a similar manner, given a text T [1 ‥ n], we let t_s denote the decimal value of the length-m substring T[s + 1 ‥ s + m], for s = 0, 1, . . . , n - m. Certainly, t_s = p if and only if T [s + 1 ‥ s + m] = P[1 ‥ m]; thus, s is a valid shift if and only if t_s = p. If we could compute p in time Θ(m) and all the t_s values in a total of Θ(n - m + 1) time,^[1] then we could determine all valid shifts s in time Θ(m) + Θ(n - m + 1) = Θ(n) by comparing p with each of the t_s's. (For the moment, let's not worry about the possibility that p and the t_s's might be very large numbers.)

We can compute p in time Θ(m) using Horner's rule (see Section 30.1):

p = P[m] + 10 (P[m - 1] + 10(P[m - 2] + · · · + 10(P[2] + 10P[1]) )).

The value t₀ can be similarly computed from T [1 ‥ m] in time Θ(m).

To compute the remaining values t₁, t₂, . . . , t_n-m in time Θ(n - m), it suffices to observe that t_s+1 can be computed from t_s in constant time, since

(32.1)

For example, if m = 5 and t_s = 31415, then we wish to remove the high-order digit T [s + 1] = 3 and bring in the new low-order digit (suppose it is T [s + 5 + 1] = 2) to obtain

Subtracting 10^m-1 T[s + 1] removes the high-order digit from t_s, multiplying the result by 10 shifts the number left one position, and adding T [s + m + 1] brings in the appropriate low-order digit. If the constant 10^m-1 is precomputed (which can be done in time O(lg m) using the techniques of Section 31.6, although for this application a straightforward O(m)-time method is quite adequate), then each execution of equation (32.1) takes a constant number of arithmetic operations. Thus, we can compute p in time Θ(m) and compute t₀, t₁, . . . , t_n-m in time Θ(n - m + 1), and we can find all occurrences of the pattern P[1 ‥ m] in the text T [1 ‥ n] with Θ(m) preprocessing time and Θ(n - m + 1) matching time.

The only difficulty with this procedure is that p and t_s may be too large to work with conveniently. If P contains m characters, then assuming that each arithmetic operation on p (which is m digits long) takes "constant time" is unreasonable. Fortunately, there is a simple cure for this problem, as shown in Figure 32.5: compute p and the t_s's modulo a suitable modulus q. Since the computation of p, t₀, and the recurrence (32.1) can all be performed modulo q, we see that we can compute p modulo q in Θ(m) time and all the t_s's modulo q in Θ(n - m + 1) time. The modulus q is typically chosen as a prime such that 10q just fits within one computer word, which allows all the necessary computations to be performed with single-precision arithmetic. In general, with a d-ary alphabet {0, 1, . . . , d - 1}, we choose q so that dq fits within a computer word and adjust the recurrence equation (32.1) to work modulo q, so that it becomes

(32.2)

where h = d^m-1 (mod q) is the value of the digit "1" in the high-order position of an m-digit text window.

Figure 32.5: The Rabin-Karp algorithm. Each character is a decimal digit, and we compute values modulo 13. (a) A text string. A window of length 5 is shown shaded. The numerical value of the shaded number is computed modulo 13, yielding the value 7. (b) The same text string with values computed modulo 13 for each possible position of a length-5 window. Assuming the pattern P = 31415, we look for windows whose value modulo 13 is 7, since 31415 ≡ 7 (mod 13). Two such windows are found, shown shaded in the figure. The first, beginning at text position 7, is indeed an occurrence of the pattern, while the second, beginning at text position 13, is a spurious hit. (c) Computing the value for a window in constant time, given the value for the previous window. The first window has value 31415. Dropping the high-order digit 3, shifting left (multiplying by 10), and then adding in the low-order digit 2 gives us the new value 14152. All computations are performed modulo 13, however, so the value for the first window is 7, and the value computed for the new window is 8.

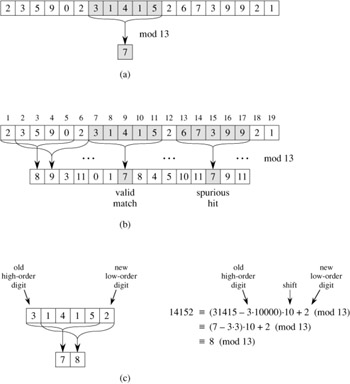
The solution of working modulo q is not perfect, however, since t_s ≡ p (mod q) does not imply that t_s = p. On the other hand, if t_s ≢ p (mod q), then we definitely have that t_s ≠ p, so that shift s is invalid. We can thus use the test t_s ≡ p (mod q) as a fast heuristic test to rule out invalid shifts s. Any shift s for which t_s ≡ p (mod q) must be tested further to see if s is really valid or we just have a spurious hit. This testing can be done by explicitly checking the condition P[1 ‥ m] = T [s + 1 ‥ s + m]. If q is large enough, then we can hope that spurious hits occur infrequently enough that the cost of the extra checking is low.

The following procedure makes these ideas precise. The inputs to the procedure are the text T , the pattern P, the radix d to use (which is typically taken to be |Σ|), and the prime q to use.

RABIN-KARP-MATCHER(T, P, d, q)
 1 n ← length[T]
 2 m ← length[P]
 3 h ← dm-1 mod q
 4 p ← 0
 5 t0 ← 0
 6 for i ← 1 to m           ▹ Preprocessing.
 7     do p ← (dp + P[i]) mod q
 8        t0 ← (dt0 + T[i]) mod q
 9 for s ← 0 to n - m       ▹ Matching.
10     do if p = ts
11           then if P[1 ‥ m] = T [s + 1 ‥ s + m]
12                   then print "Pattern occurs with shift" s
13        if s < n - m
14           then ts+1 ← (d(ts - T[s + 1]h) + T[s + m + 1]) mod q

The procedure RABIN-KARP-MATCHER works as follows. All characters are interpreted as radix-d digits. The subscripts on t are provided only for clarity; the program works correctly if all the subscripts are dropped. Line 3 initializes h to the value of the high-order digit position of an m-digit window. Lines 4-8 compute p as the value of P[1 ‥ m] mod q and t₀ as the value of T [1 ‥ m] mod q. The for loop of lines 9-14 iterates through all possible shifts s, maintaining the following invariant:

• Whenever line 10 is executed, t_s = T[s + 1‥ s + m] mod q.

If p = t_s in line 10 (a "hit"), then we check to see if P[1 ‥ m] = T [s + 1 ‥ s + m] in line 11 to rule out the possibility of a spurious hit. Any valid shifts found are printed out on line 12. If s < n - m (checked in line 13), then the for loop is to be executed at least one more time, and so line 14 is first executed to ensure that the loop invariant holds when line 10 is again reached. Line 14 computes the value of t_s+1 mod q from the value of t_s mod q in constant time using equation (32.2) directly.

RABIN-KARP-MATCHER takes Θ(m) preprocessing time, and its matching time is Θ((n - m + 1)m) in the worst case, since (like the naive string-matching algorithm) the Rabin-Karp algorithm explicitly verifies every valid shift. If P = a^m and T = aⁿ, then the verifications take time Θ((n - m + 1)m), since each of the n - m + 1 possible shifts is valid.

In many applications, we expect few valid shifts (perhaps some constant c of them); in these applications, the expected matching time of the algorithm is only O((n - m + 1) + cm) = O(n+m), plus the time required to process spurious hits. We can base a heuristic analysis on the assumption that reducing values modulo q acts like a random mapping from Σ* to Z_q. (See the discussion on the use of division for hashing in Section 11.3.1. It is difficult to formalize and prove such an assumption, although one viable approach is to assume that q is chosen randomly from integers of the appropriate size. We shall not pursue this formalization here.) We can then expect that the number of spurious hits is O(n/q), since the chance that an arbitrary t_s will be equivalent to p, modulo q, can be estimated as 1/q. Since there are O(n) positions at which the test of line 10 fails and we spend O(m) time for each hit, the expected matching time taken by the Rabin-Karp algorithm is

O(n) + O(m(v + n/q)),

where v is the number of valid shifts. This running time is O(n) if v = O(1) and we choose q ≥ m. That is, if the expected number of valid shifts is small (O(1)) and the prime q is chosen to be larger than the length of the pattern, then we can expect the Rabin-Karp procedure to use only O(n + m) matching time. Since m ≤ n, this expected matching time is O(n).

Exercises 32.2-1

Working modulo q = 11, how many spurious hits does the Rabin-Karp matcher encounter in the text T = 3141592653589793 when looking for the pattern P = 26?

Exercises 32.2-2

How would you extend the Rabin-Karp method to the problem of searching a text string for an occurrence of any one of a given set of k patterns? Start by assuming that all k patterns have the same length. Then generalize your solution to allow the patterns to have different lengths.

Exercises 32.2-3

Show how to extend the Rabin-Karp method to handle the problem of looking for a given m × m pattern in an n × n array of characters. (The pattern may be shifted vertically and horizontally, but it may not be rotated.)

Exercises 32.2-4

Alice has a copy of a long n-bit file A = 〈a_n-1, a_n-2, . . . , a₀〉, and Bob similarly has an n-bit file B = 〈b_n-1, b_n-2, . . . , b₀〉. Alice and Bob wish to know if their files are identical. To avoid transmitting all of A or B, they use the following fast probabilistic check. Together, they select a prime q > 1000n and randomly select an integer x from {0, 1, . . . , q - 1}. Then, Alice evaluates

and Bob similarly evaluates B(x). Prove that if A ≠ B, there is at most one chance in 1000 that A(x) = B(x), whereas if the two files are the same, A(x) is necessarily the same as B(x). (Hint: See Exercise 31.4-4.)