| < Day Day Up > |
The probability of having at least, or at most, k successes in n Bernoulli trials, each with probability p of success, is often of more interest than the probability of having exactly k successes. In this section, we investigate the tails of the binomial distribution: the two regions of the distribution b(k; n, p) that are far from the mean np. We shall prove several important bounds on (the sum of all terms in) a tail.
We first provide a bound on the right tail of the distribution b(k; n, p). Bounds on the left tail can be determined by inverting the roles of successes and failures.
Consider a sequence of n Bernoulli trials, where success occurs with probability p. Let X be the random variable denoting the total number of successes. Then for 0 ≤ k ≤ n, the probability of at least k successes is
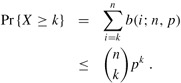
Proof For S ⊆ {1, 2,..., n}, we let AS denote the event that the ith trial is a success for every i ∈ S. Clearly Pr {AS} = pk if |S| = k. We have
where the inequality follows from Boole's inequality (C.18).
The following corollary restates the theorem for the left tail of the binomial distribution. In general, we shall leave it to the reader to adapt the proofs from one tail to the other.
Our next bound concerns the left tail of the binomial distribution. Its corollary shows that, far from the mean, the left tail diminishes exponentially.
Consider a sequence of n Bernoulli trials, where success occurs with probability p and failure with probability q = 1 - p. Let X be the random variable denoting the total number of successes. Then for 0 < k < np, the probability of fewer than k successes is
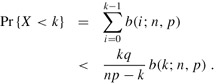
Proof We bound the series ![]() by a geometric series using the technique from Section A.2, page 1064. For i = 1, 2,..., k, we have from equation (C.40),
by a geometric series using the technique from Section A.2, page 1064. For i = 1, 2,..., k, we have from equation (C.40),
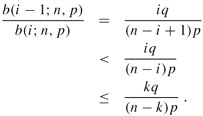
If we let
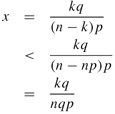
it follows that
b(i - 1; n, p) < xb(i; n, p)
for 0 < i ≤ k. Iteratively applying this inequality k - i times, we obtain
b(i; n, p) < xk-i b(k; n, p)
for 0 ≤ i < k, and hence
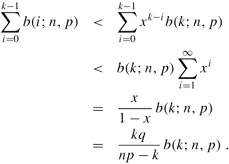
Consider a sequence of n Bernoulli trials, where success occurs with probability p and failure with probability q = 1 - p. Then for 0 < k ≤ np/2, the probability of fewer than k successes is less than one half of the probability of fewer than k + 1 successes.
Proof Because k ≤ np/2, we have
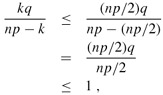
since q ≤ 1. Letting X be the random variable denoting the number of successes, Theorem C.4 implies that the probability of fewer than k successes is
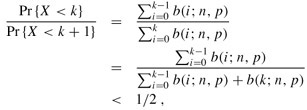
since ![]()
Bounds on the right tail can be determined similarly. Their proofs are left as Exercise C.5-2.
Consider a sequence of n Bernoulli trials, where success occurs with probability p. Let X be the random variable denoting the total number of successes. Then for np < k < n, the probability of more than k successes is
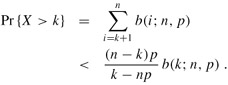
Consider a sequence of n Bernoulli trials, where success occurs with probability p and failure with probability q = 1 - p. Then for (np + n)/2 < k < n, the probability of more than k successes is less than one half of the probability of more than k - 1 successes.
The next theorem considers n Bernoulli trials, each with a probability pi of success, for i = 1, 2,...,n. As the subsequent corollary shows, we can use the theorem to provide a bound on the right tail of the binomial distribution by setting pi = p for each trial.
Consider a sequence of n Bernoulli trials, where in the ith trial, for i = 1, 2,...,n, success occurs with probability pi and failure occurs with probability qi = 1 - pi. Let X be the random variable describing the total number of successes, and let μ = E [X]. Then for r > μ,
Proof Since for any α > 0, the function eαx is strictly increasing in x,
where α will be determined later. Using Markov's inequality (C.29), we obtain
The bulk of the proof consists of bounding E[eα(X - μ)] and substituting a suitable value for α in inequality (C.42). First, we evaluate E[eα(X - μ)]. Using the notation of Section 5.2, let Xi = I {the ith Bernoulli trial is a success} for i = 1, 2,...,n; that is, Xi is the random variable that is 1 if the ith Bernoulli trial is a success and 0 if it is a failure. Thus,
and by linearity of expectation,
which implies
To evaluate E[eα(X - μ)], we substitute for X - μ, obtaining
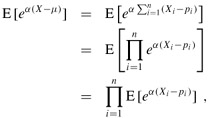
which follows from (C.23), since the mutual independence of the random variables Xi implies the mutual independence of the random variables ![]() (see Exercise C.3-5). By the definition of expectation,
(see Exercise C.3-5). By the definition of expectation,
where exp(x) denotes the exponential function: exp(x) = ex. (Inequality (C.43) follows from the inequalities α > 0, qi ≤ 1, eαqi ≤ eα, and e αpi ≤ 1, and the last line follows from inequality (3.11)). Consequently,
since ![]() . Therefore, from equation (C.41) and inequalities (C.42) and (C.44), it follows that
. Therefore, from equation (C.41) and inequalities (C.42) and (C.44), it follows that
Choosing α = ln(r/μ) (see Exercise C.5-7), we obtain
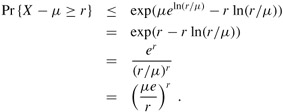
When applied to Bernoulli trials in which each trial has the same probability of success, Theorem C.8 yields the following corollary bounding the right tail of a binomial distribution.
Consider a sequence of n Bernoulli trials, where in each trial success occurs with probability p and failure occurs with probability q = 1 - p. Then for r > np,
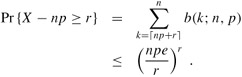
Proof By equation (C.36), we have μ = E [X] = np.
Which is less likely: obtaining no heads when you flip a fair coin n times, or obtaining fewer than n heads when you flip the coin 4n times?
Show that the conditions of Theorem C.8 imply that
Similarly, show that the conditions of Corollary C.9 imply that
Consider a sequence of n Bernoulli trials, where in the ith trial, for i = 1, 2,..., n, success occurs with probability pi and failure occurs with probability qi = 1 - pi. Let X be the random variable describing the total number of successes, and let μ = E [X]. Show that for r ≥ 0,
(Hint: Prove that ![]() . Then follow the outline of the proof of Theorem C.8, using this inequality in place of inequality (C.43).)
. Then follow the outline of the proof of Theorem C.8, using this inequality in place of inequality (C.43).)
In this problem, we investigate the effect of various assumptions on the number of ways of placing n balls into b distinct bins.
Suppose that the n balls are distinct and that their order within a bin does not matter. Argue that the number of ways of placing the balls in the bins is bn.
Suppose that the balls are distinct and that the balls in each bin are ordered. Prove that there are exactly (b + n - 1)!/(b - 1)! ways to place the balls in the bins. (Hint: Consider the number of ways of arranging n distinct balls and b - 1 indistinguishable sticks in a row.)
Suppose that the balls are identical, and hence their order within a bin does not matter. Show that the number of ways of placing the balls in the bins is ![]() . (Hint: Of the arrangements in part (b), how many are repeated if the balls are made identical?)
. (Hint: Of the arrangements in part (b), how many are repeated if the balls are made identical?)
Suppose that the balls are identical and that no bin may contain more than one ball. Show that the number of ways of placing the balls is ![]() .
.
Suppose that the balls are identical and that no bin may be left empty. Show that the number of ways of placing the balls is ![]() .
.
| < Day Day Up > |