Cholesky factorization

In linear algebra, a matrix decomposition or matrix factorization is a factorization of a matrix into a product of matrices. There are many different matrix decompositions. One of them is Cholesky Decomposition.
The Cholesky decomposition or Cholesky factorization is a decomposition of a Hermitian, positive-definite matrix into the product of a lower triangular matrix and its conjugate transpose. The Cholesky decomposition is roughly twice as efficient as the LU decomposition for solving systems of linear equations.
The Cholesky decomposition of a Hermitian positive-definite matrix A is a decomposition of the form A = [L][L]^T, where L is a lower triangular matrix with real and positive diagonal entries, and L^T denotes the conjugate transpose of L. Every Hermitian positive-definite matrix (and thus also every real-valued symmetric positive-definite matrix) has a unique Cholesky decomposition.
 

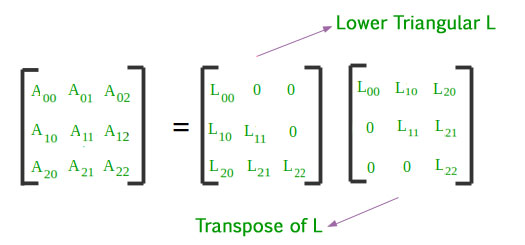
Every symmetric, positive definite matrix A can be decomposed into a product of a unique lower triangular matrix L and its transpose: A = L L^T 
The following formulas are obtained by solving above lower triangular matrix and its transpose. These are the basis of Cholesky Decomposition Algorithm :
 

[Tex]L_{i,j}=\frac{1}{L_{j,j}}(A_{i,j}-\sum_{k=0}^{j-1}L_{i,k}L_{j,k})   [/Tex]

#include <iostream.h>
#include <stdlib.h>
#include <conio.h>
#include <math.h>
double a[10][10],L[10][10],s;
int i,j,k,n;

void main(){
	clrscr();
	cout<<"\nDati dimensiunea matricei A: n=";cin>>n;
	cout<<"\nDati matricea A:\n";
	for(i=1;i<=n;i++)
		for(j=1;j<=n;j++){
		cout<<"a["<<i<<"]["<<j<<"]=";cin>>a[i][j];
	}
	a[1][1]=sqrt(a[1][1]);
	for(i=2;i<=n;i++)
		a[i][1]=a[i][1]/a[1][1];
	for(j=2;j<=n-1;j++){
		s=0;
		for(k=1;k<=j-1;k++)
			s+=a[j][k]*a[j][k];
		a[j][j]=sqrt(a[j][j]-s);

		for(i=j+1;i<=n;i++){
			s=0;
			for(k=1;k<=j-1;k++)
				s+=a[i][k]*a[j][k];
			a[i][j]=(a[i][j]-s)/a[j][j];
		}
	}
	s=0;
	for(k=1;k<=n-1;k++)
			s+=a[n][k]*a[n][k];
	a[n][n]=sqrt(a[n][n]-s);
			for(i=1;i<n;i++)
		for(j=i+1;j<=n;j++)
		a[i][j]=0;
	cout<<"\nMatricea L este:\n";
	for(i=1;i<=n;i++){
		for(j=1;j<=n;j++)
			cout<<a[i][j]<<"  ";
		cout<<"\n";
	}

	getch();
}

2,761 total views, 1 views today